题目内容
(2012•道里区三模)在平面直角坐标系中,已知A1(-
,0),A2(
,0),P(x,y),M(x,1),N(x,-2),若实数λ使得λ2
•
=
•
(O为坐标原点).
(Ⅰ) 求P点的轨迹方程,并讨论P点的轨迹类型;
(Ⅱ) 当λ=
时,是否存在过点B(0,2)的直线l与(Ⅰ)中P点的轨迹交于不同的两点E,F(E在B,F之间),且[
>1.若存在,求出该直线的斜率的取值范围,若不存在,说明理由.
| 2 |
| 2 |
| OM |
| ON |
| A1P |
| A2P |
(Ⅰ) 求P点的轨迹方程,并讨论P点的轨迹类型;
(Ⅱ) 当λ=
| ||
| 2 |
| S△OBE |
| S△EOF |
分析:(Ⅰ) 由题设条件,知(1-λ2)x2+y2=2(1-λ2),由此进行分类讨论能得到P点的轨迹类型.
(Ⅱ)由λ=
,知P点轨迹方程为
+y2=1.S△OBE:S△OBF=|x1|:|x2|,由
>1,得
<
<1.设直线EF直线方程为y=kx+2,联立方程可得:(1+2k2)x2+8kx+6=0,由此能够推导出直线的斜率的取值范围.
(Ⅱ)由λ=
| ||
| 2 |
| x2 |
| 2 |
| S△OBE |
| S△EOF |
| 1 |
| 2 |
| |x1| |
| |x2| |
解答:解:(Ⅰ)∵A1(-
,0),A2(
,0),P(x,y),M(x,1),N(x,-2),
实数λ使得λ2
•
=
•
(O为坐标原点).
∴(1-λ2)x2+y2=2(1-λ2),
①λ=±1时方程为y=0轨迹为一条直线,
②λ=0时方程为x2+y2=2轨迹为圆,
③λ∈(-1,0)∪(0,1)时方程为
+
=1轨迹为椭圆,
④λ∈(-∞,-1)∪(1,+∞)时方程为
-
=1轨迹为双曲线.…(6分)
(Ⅱ)∵λ=
,∴P点轨迹方程为
+y2=1.
S△OBE:S△OBF=|x1|:|x2|
由
>1,得
>1,
则
>1,∴
<
<1.
设直线EF直线方程为y=kx+2,
联立方程可得:(1+2k2)x2+8kx+6=0,
∵△=64k2-24(1+2k2)>0,∴k2>
,
∵x1,x2同号,∴
=
x1+x2=-
,x1x2=
,…(8分)
设
=m,则
=
=
∈(4,
)
<k2<
,k∈(
,
)∪(-
,-
).…(12分)
| 2 |
| 2 |
实数λ使得λ2
| OM |
| ON |
| A1P |
| A2P |
∴(1-λ2)x2+y2=2(1-λ2),
①λ=±1时方程为y=0轨迹为一条直线,
②λ=0时方程为x2+y2=2轨迹为圆,
③λ∈(-1,0)∪(0,1)时方程为
| x2 |
| 2 |
| y2 |
| 2(1-λ2) |
④λ∈(-∞,-1)∪(1,+∞)时方程为
| x2 |
| 2 |
| y2 |
| 2(λ2-1) |
(Ⅱ)∵λ=
| ||
| 2 |
| x2 |
| 2 |
S△OBE:S△OBF=|x1|:|x2|
由
| S△OBE |
| S△EOF |
| S△OBE |
| S△OBF-S△OBE |
则
| |x1| |
| |x2|-|x1| |
| 1 |
| 2 |
| |x1| |
| |x2| |
设直线EF直线方程为y=kx+2,
联立方程可得:(1+2k2)x2+8kx+6=0,
∵△=64k2-24(1+2k2)>0,∴k2>
| 3 |
| 2 |
∵x1,x2同号,∴
| |x1| |
| |x2| |
| x1 |
| x2 |
| 8k |
| 1+2k2 |
| 6 |
| 1+2k2 |
设
| x1 |
| x2 |
| (x1+x2)2 |
| x1x2 |
| (m+1)2 |
| m |
| 32k2 |
| 3+6k2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 27 |
| 10 |
| ||
| 2 |
3
| ||
| 10 |
3
| ||
| 10 |
| ||
| 2 |
点评:本题考查曲线类型的判断,考查直线的斜率的取值范围的求法,解题时要认真审题,仔细解答,注意分类讨论思想和等价转化思想的合理运用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
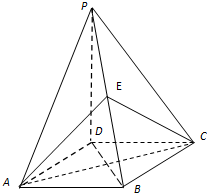 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=