题目内容
(本小题满分12分)在 中,顶点
中,顶点 ,
, ,
, 、
、 分别是
分别是 的重心和内心,且
的重心和内心,且 .
.
 求顶点
求顶点 的轨迹
的轨迹 的方程;
的方程;
 过点
过点 的直线交曲线
的直线交曲线 于
于 、
、 两点,
两点, 是直线
是直线 上一点,设直线
上一点,设直线 、
、 、
、 的斜率分别为
的斜率分别为 ,
, ,
, ,求证:
,求证: .
.
(1) 
 ; (2) 详见解析
; (2) 详见解析
【解析】
试题分析:(1) 根据题中三角形内心的含义可知: ,又由条件:
,又由条件: ,可见I和G的纵坐标相等,又
,可见I和G的纵坐标相等,又 ,
, ,代入化简得:
,代入化简得: ,根据椭圆的定义得:顶点
,根据椭圆的定义得:顶点 的轨迹是以
的轨迹是以 为焦点,4为长轴长的椭圆,其中
为焦点,4为长轴长的椭圆,其中 进而其方程,不过要注意去掉顶点噢; (2) 根据题意可设出直线方程,进而表示出点
进而其方程,不过要注意去掉顶点噢; (2) 根据题意可设出直线方程,进而表示出点 的坐标,不过要注意分斜率是否存在:当直线
的坐标,不过要注意分斜率是否存在:当直线 斜率存在时,设直线
斜率存在时,设直线 且
且 ,
, ,
, ,与椭圆联立方程组,运用韦达定理可得
,与椭圆联立方程组,运用韦达定理可得 ,
, .由题意:
.由题意: ,
, ,
, .化简得
.化简得

 .当直线
.当直线 斜率不存在时,易得结论.
斜率不存在时,易得结论.
试题解析:(1) 已知 ,且
,且 ,
, ,
,
其中 为内切圆半径,化简得:
为内切圆半径,化简得: ,顶点
,顶点 的轨迹是以
的轨迹是以 为焦点,
为焦点,
4为长轴长的椭圆(去掉长轴端点),其中
进而其方程为
 . (5分)
. (5分)
(2) 证明:当直线 斜率存在时,设直线
斜率存在时,设直线 且
且 ,
, ,
,
联立 可得
可得 ,
, . (8分)
. (8分)
由题意: ,
, ,
, .
.


当直线 斜率不存在时,
斜率不存在时, ,
,
综上可得 . (12分)
. (12分)
考点:1.轨迹方程的求法;2.椭圆方程的求法;3.直线与圆锥曲线的位置关系

练习册系列答案
相关题目
 的离心率为2,则其渐近线的斜率为( )
的离心率为2,则其渐近线的斜率为( ) B.
B. C.
C. D.
D.
 与双曲线
与双曲线 相交于
相交于 两点,则
两点,则 =( )
=( ) 4 B.
4 B. C.
C. D.
D.
 ,则
,则 ( )
( )  B.
B. C.
C. D.
D.
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 的三条侧棱
的三条侧棱 ,
, ,
, 两两互相垂直且长都相等,其外接球半径为
两两互相垂直且长都相等,其外接球半径为 ,则三棱锥的表面积为 .
,则三棱锥的表面积为 . 、
、 、
、 、
、 ,右图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )
,右图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )
 B.
B. C.
C. D.
D.
 的外接球半径为
的外接球半径为 ,过棱
,过棱 作该球的截面,则截面面积的最小值为 .
作该球的截面,则截面面积的最小值为 .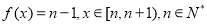 ,函数
,函数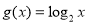 ,则方程
,则方程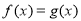 实数根的个数是( ).
实数根的个数是( ). 个 (B)
个 (B)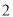 个 (C)
个 (C)  个 (D)
个 (D) 个
个