题目内容
在△ABC中,已知角A、B、C所对的边分别是a、b、c,且a=2, ,设∠C=θ.
,设∠C=θ.
(1)θ表示b;
(2)若 ,求
,求 的值.
的值.
(1)在△ABC中,a=2,∠A= ,∠B=π-∠C=π-
,∠B=π-∠C=π- -θ
-θ
由正弦定得  ,b=2
,b=2 sin(
sin( -θ )
-θ )
(2)△ABC中,再由正弦定得 ,c=2
,c=2 sinθ.
sinθ.
故有 =
= =8
=8
因为tanθ=- ,所以
,所以 <θ<π,所以 sinθ=
<θ<π,所以 sinθ= ,cosθ=
,cosθ=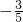
又 sin( -θ )=sin
-θ )=sin cosθ-cos
cosθ-cos sinθ=
sinθ=
所以 =8×
=8× ×(
×(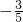 )=
)=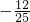
分析:(1)在△ABC中,先求出∠B=π-∠C=π-
 -θ,由正弦定
-θ,由正弦定 求出b.
求出b.(2)△ABC中,再由正弦定
 求出 c,根据两个向量的数量积的定义求出
求出 c,根据两个向量的数量积的定义求出 =8
=8 ,再由tanθ=-
,再由tanθ=- ,求出sinθ 和 cosθ 的值,可得
,求出sinθ 和 cosθ 的值,可得sin(
 -θ )的值,从而求得 8
-θ )的值,从而求得 8 的值,即为所求.
的值,即为所求.点评:本题主要考查正弦定理、两角和差的正弦公式的应用,两个向量的数量积的定义,求出sin(
 -θ )=
-θ )= ,是解题的关键.
,是解题的关键. 
练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目