题目内容
边长为a的菱形ABCD中锐角A=θ，现沿对角线BD折成60°的二面角，翻折后|AC|=
a，则锐角A是
- A.
- B.
- C.
- D.
C
分析：先确定二面角C-BD-A的平面角，再计算AO的长，即可求得结论．
解答：取BD的中点O，连接OC、OA，则∠COA为二面角C-BD-A的平面角，即∠COA=60°
∵|AC|=a，∴|AO|=a
∵菱形ABCD中AD=a，∴∠ADB=
∴∠A=
故选C．
点评：本题考查二面角的平面角，考查学生的计算能力，确定二面角的平面角是关键．
分析：先确定二面角C-BD-A的平面角，再计算AO的长，即可求得结论．
解答：取BD的中点O，连接OC、OA，则∠COA为二面角C-BD-A的平面角，即∠COA=60°
∵|AC|=
a，∴|AO|=a∵菱形ABCD中AD=a，∴∠ADB=
∴∠A=
故选C．
点评：本题考查二面角的平面角，考查学生的计算能力，确定二面角的平面角是关键．
练习册系列答案
优生乐园系列答案
相关题目
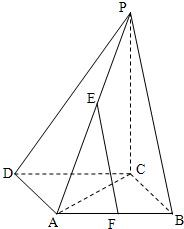如图，在边长为a的菱形ABCD中，∠ABC=60°，PC⊥面ABCD，E，F是PA和AB的中点．
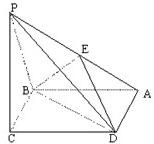已知四棱锥P-ABCD的底面是边长为a的菱形，∠ABC=120°，又PC⊥平面ABCD，PC=a，E是PA的中点．
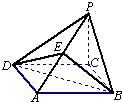如图，四棱锥P-ABCD的底面是边长为a的菱形，∠ABC=60°，PC⊥平面ABCD，PC=a，E为PA中点，
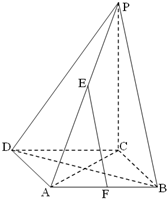如图，在边长为a的菱形ABCD中，∠ABC=60°，PC⊥面ABCD，PC=2a，E、F分别是PA和AB的中点．
如图，斜三棱柱ABC-A1B1C1的底面是直角三角形，AC⊥CB，∠ABC=45°，侧面A1ABB1是边长为a的菱形，且垂直于底面ABC，∠A1AB=60°，E、F分别是AB1、BC的中点．