题目内容
 已知椭圆C:
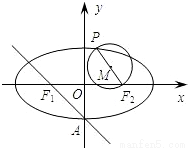
已知椭圆C: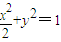 的左、右焦点分别为F1,F2,下顶点为A,点P是椭圆上任一点,⊙M是以PF2为直径的圆.
的左、右焦点分别为F1,F2,下顶点为A,点P是椭圆上任一点,⊙M是以PF2为直径的圆.(Ⅰ)当⊙M的面积为
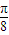 时,求PA所在直线的方程;
时,求PA所在直线的方程;(Ⅱ)当⊙M与直线AF1相切时,求⊙M的方程;
(Ⅲ)求证:⊙M总与某个定圆相切.
【答案】分析:(Ⅰ)根据椭圆方程求得焦点,顶点的坐标,设出点P的坐标,进而表示出|PF2|的长度进而根据圆M的面积求得x1,求得P的坐标,则PA所在的直线方程可得.
(Ⅱ)根据点M到直线AF1的距离求得x1和y1的关系式,进而与椭圆方程联立求得x1,进而求得M的坐标则圆的方程可得.
(Ⅲ)首先表示出OM的长度,以及圆M的半径,进而求得OM=r1-r2,推断出⊙M和以原点为圆心,半径为r1= (长半轴)的圆相内切.
(长半轴)的圆相内切.
解答:解:(Ⅰ)易得F1(-1,0),F2(1,0),A(0,-1),设点P(x1,y1),
则 ,
,
所以
又⊙M的面积为 ,∴
,∴ ,
,
解得x1=1,∴ ,
,
∴PA所在直线方程为 或
或
(Ⅱ)因为直线AF1的方程为x+y+1=0,且 到直线AF1的距离为
到直线AF1的距离为
化简得y1=-1-2x1,联立方程组 ,
,
解得x1=0或
∴当x1=0时,可得 ,
,
∴⊙M的方程为 ;
;
当 时,可得
时,可得 ,
,
∴⊙M的方程为
(Ⅲ)⊙M始终和以原点为圆心,半径为r1= (长半轴)的圆(记作⊙O)相切
(长半轴)的圆(记作⊙O)相切
证明:因为
= ,
,
又⊙M的半径r2=MF2= ,
,
∴OM=r1-r2,∴⊙M和⊙O相内切.
点评:本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.
(Ⅱ)根据点M到直线AF1的距离求得x1和y1的关系式,进而与椭圆方程联立求得x1,进而求得M的坐标则圆的方程可得.
(Ⅲ)首先表示出OM的长度,以及圆M的半径,进而求得OM=r1-r2,推断出⊙M和以原点为圆心,半径为r1=
 (长半轴)的圆相内切.
(长半轴)的圆相内切.解答:解:(Ⅰ)易得F1(-1,0),F2(1,0),A(0,-1),设点P(x1,y1),
则
 ,
,所以

又⊙M的面积为
 ,∴
,∴ ,
,解得x1=1,∴
 ,
,∴PA所在直线方程为
 或
或
(Ⅱ)因为直线AF1的方程为x+y+1=0,且
 到直线AF1的距离为
到直线AF1的距离为
化简得y1=-1-2x1,联立方程组
 ,
,解得x1=0或

∴当x1=0时,可得
 ,
,∴⊙M的方程为
 ;
;当
 时,可得
时,可得 ,
,∴⊙M的方程为

(Ⅲ)⊙M始终和以原点为圆心,半径为r1=
 (长半轴)的圆(记作⊙O)相切
(长半轴)的圆(记作⊙O)相切证明:因为

=
 ,
,又⊙M的半径r2=MF2=
 ,
,∴OM=r1-r2,∴⊙M和⊙O相内切.
点评:本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 (2013•临沂二模)
(2013•临沂二模) 的左、右焦点分别为F1,F2,O为原点.
的左、右焦点分别为F1,F2,O为原点.
 的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线
的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线 相切.
相切. 的对称点,动点M满足
的对称点,动点M满足 . 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由.
. 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由. 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,点A是椭圆上任一点,
,点A是椭圆上任一点, 的周长为
的周长为 .
. 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于 两点,记
两点,记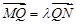 ,若在线段
,若在线段 上取一点R,使得
上取一点R,使得 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
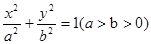 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为 ,
, ,离心率
,离心率 。
。 ,
, ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两点,证明直线
两点,证明直线 与直线
与直线 的交点在直线
的交点在直线 上。
上。