题目内容
设数列an的首项 ,且
,且 ,记
,记
(1)求a2•a3
(2)判断数列{bn}是否为等比数列,并证明你的结论;
(3)证明b1+3b2+5b3 .
.
(1)解:由题意,a2=a1+ =
= ,a3=
,a3= a2=
a2= ---------------------------------(4分)
---------------------------------(4分)
(2)解:{bn}是等比数列
证明如下:因为bn+1=a2n+1- =
= a2n-
a2n- =
= (a2n-1-
(a2n-1- )=
)= bn,(n∈N*)
bn,(n∈N*)
所以{bn}是首项为 ,公比为
,公比为 的等比数列
的等比数列
所以 -----(8分)
-----(8分)
(3)证明:(2n-1)bn=
令Sn=b1+3b2+5b3+…+ =
= +3•
+3• +…+
+…+ ①,则
①,则
 Sn=
Sn= +3•
+3•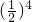 +…+(2n-3)•
+…+(2n-3)•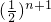 +
+ ②
②
①-②可得 Sn=
Sn= +2•
+2• +2•
+2•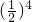 +…+2•
+…+2•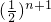 -
-
∴Sn= ,显然小于
,显然小于 ---------(13分)
---------(13分)
分析:(1)利用数列递推式,代入计算可得结论;
(2){bn}是等比数列,利用 ,代入计算可可以证明;
,代入计算可可以证明;
(3)利用错位相减法求和,即可证得结论.
点评:本题考查数列递推式,考查等比数列的证明,考查错位相减法,考查学生的计算能力,属于中档题.
 =
= ,a3=
,a3= a2=
a2= ---------------------------------(4分)
---------------------------------(4分)(2)解:{bn}是等比数列
证明如下:因为bn+1=a2n+1-
 =
= a2n-
a2n- =
= (a2n-1-
(a2n-1- )=
)= bn,(n∈N*)
bn,(n∈N*)所以{bn}是首项为
 ,公比为
,公比为 的等比数列
的等比数列所以
 -----(8分)
-----(8分)(3)证明:(2n-1)bn=

令Sn=b1+3b2+5b3+…+
 =
= +3•
+3• +…+
+…+ ①,则
①,则 Sn=
Sn= +3•
+3•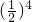 +…+(2n-3)•
+…+(2n-3)•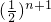 +
+ ②
②①-②可得
 Sn=
Sn= +2•
+2• +2•
+2•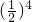 +…+2•
+…+2•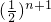 -
-
∴Sn=
 ,显然小于
,显然小于 ---------(13分)
---------(13分)分析:(1)利用数列递推式,代入计算可得结论;
(2){bn}是等比数列,利用
 ,代入计算可可以证明;
,代入计算可可以证明;(3)利用错位相减法求和,即可证得结论.
点评:本题考查数列递推式,考查等比数列的证明,考查错位相减法,考查学生的计算能力,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
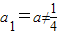 ,且
,且 记
记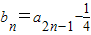 ,n=1,2,3,….
,n=1,2,3,…. ,且
,且 ,记
,记
 .
.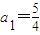 ,且an+1=
,且an+1= ,记bn=a2n-1
,记bn=a2n-1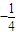 ,n=1,2,3,…
,n=1,2,3,…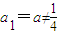 ,且
,且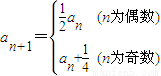 ,n∈N*,记
,n∈N*,记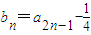 ,
,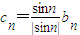 ,n∈N*.
,n∈N*.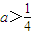 时,数列{cn}前n项和为Sn,求Sn最值.
时,数列{cn}前n项和为Sn,求Sn最值.