题目内容
已知岛A南偏西38°方向，距岛3海里的B处有一艘缉私艇．岛A处的一艘走私船正以10海里/小时的速度向岛北偏西22°方向行驶，问缉私艇朝何方向以多大速度行驶，恰好用0.5小时能截住该走私船？（参考数据：
，
．）
，．）
解：由题意AC射线即为走私船航行路线． 假设我巡逻艇恰在C处截获走私船，我巡逻艇的速度为每小时v海里，则BC=0.5v，AC=5．
依题意，∠BAC=180°﹣38°﹣22°=120°，
由余弦定理：BC2=AB2+AC2﹣2
AB
AC
cos120°，
∴BC=7
∵BC=0.5v，
∴v=7海里/h，
又由正弦定理，sin∠ABC=
，
∴∠ABC=38°，
∵∠BAD=38°，
∴BC∥AD
即我巡逻艇须用每小时14海里的速度向正北方向航行才能恰用0.5小时在C处截住该走私船
依题意，∠BAC=180°﹣38°﹣22°=120°，
由余弦定理：BC2=AB2+AC2﹣2
ABACcos120°，∴BC=7
∵BC=0.5v，
∴v=7海里/h，
又由正弦定理，sin∠ABC=
，∴∠ABC=38°，
∵∠BAD=38°，
∴BC∥AD
即我巡逻艇须用每小时14海里的速度向正北方向航行才能恰用0.5小时在C处截住该走私船
练习册系列答案
全能测控期末小状元系列答案
相关题目
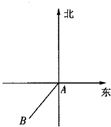（2012•河北模拟）已知岛A南偏西38°方向，距岛3海里的B处有一艘缉私艇．岛A处的一艘走私船正以10海里/小时的速度向岛北偏西22°方向行驶，问缉私艇朝何方向以多大速度行驶，恰好用0.5小时能截住该走私船？（参考数据：
，
．）
，
．）
，
．）
，
．）