题目内容
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsinA=3csinB,a=3,cosB=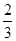
.
(1)求b的值;
(2)求sin（2B-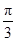
）的值.
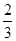.(1)求b的值;
(2)求sin（2B-
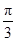）的值.(1) 
(2) 
(2) 解:(1)在△ABC中,由
=
,可得bsinA=asinB.
又由bsinA=3csinB,
可得a=3c,又a=3,故c=1.
由b2=a2+c2-2accosB,
cosB=
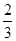,可得b=.(2)由cosB=
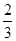,得sinB=
,从而得cos 2B=2cos2B-1=-
,sin2B=2sinBcosB=
.所以sin（2B-
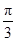）=sin2Bcos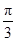-cos2Bsin=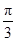
.
练习册系列答案
相关题目
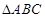的内角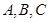
所对边的长分别为
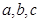.若
,则
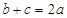则角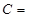
_____.
，BC＝1，sinC＝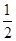
，AB＝
，BC＝3，则sin∠BAC＝( )
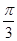，边BC＝2
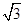.设内角B＝x，周长为y，则y＝f(x)的最大值是________．
，则AC＝________．