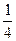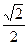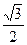题目内容
给定椭圆C: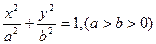 ,称圆心在原点O、半径为
,称圆心在原点O、半径为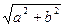 的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为
的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为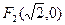 ,其短轴上的一个端点到
,其短轴上的一个端点到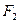 距离为
距离为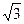 ;
;
(1)、求椭圆C的方程及其“伴椭圆”的方程;
(2)、若倾斜角为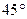 的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
(3)、若点P是椭圆C“伴椭圆”上一动点,过点P作直线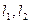 ,使得
,使得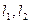 与椭圆C都只有一个公共点,求证:
与椭圆C都只有一个公共点,求证: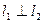 。
。
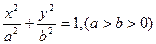 ,称圆心在原点O、半径为
,称圆心在原点O、半径为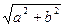 的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为
的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为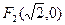 ,其短轴上的一个端点到
,其短轴上的一个端点到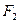 距离为
距离为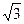 ;
;(1)、求椭圆C的方程及其“伴椭圆”的方程;
(2)、若倾斜角为
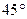 的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。(3)、若点P是椭圆C“伴椭圆”上一动点,过点P作直线
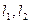 ,使得
,使得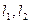 与椭圆C都只有一个公共点,求证:
与椭圆C都只有一个公共点,求证: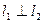 。
。解:(1)因为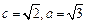 ,所以
,所以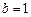 ……………………………………………2分
……………………………………………2分
所以椭圆的方程为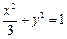 ,伴随圆的方程为
,伴随圆的方程为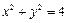 .………………4分
.………………4分
(2)设直线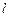 的方程
的方程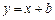 ,由
,由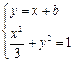 得
得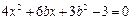
由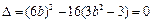 得
得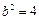 …………………………6分
…………………………6分
圆心到直线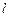 的距离为
的距离为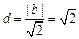 ,所以
,所以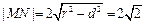 ………………………………8分
………………………………8分
(3)①、当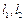 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设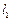 无斜率,
无斜率,
因为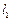 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为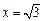 或
或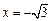 ,
,
当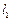 方程为
方程为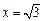 时,此时
时,此时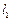 与伴随圆交于点
与伴随圆交于点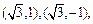
此时经过点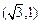 (或
(或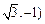 且与椭圆只有一个公共点的直线是
且与椭圆只有一个公共点的直线是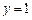 (或
(或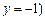 ,
,
即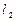 为
为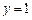 (或
(或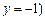 ,显然直线
,显然直线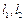 垂直;
垂直;
同理可证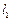 方程为
方程为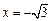 时,直线
时,直线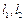 垂直.…………………………10分
垂直.…………………………10分
②、当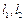 都有斜率时,设点
都有斜率时,设点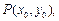 其中
其中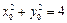 ,
,
设经过点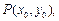 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为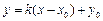 ,
,
由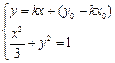 ,消去
,消去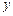 得到
得到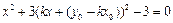 ,
,
即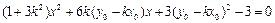 ,……………………12分
,……………………12分
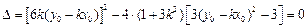 ,
,
经过化简得到: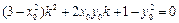 ,
,
因为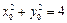 ,所以有
,所以有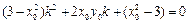 ,…………………14分
,…………………14分
设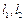 的斜率分别为
的斜率分别为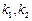 ,因为
,因为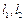 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,
所以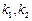 满足方程
满足方程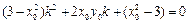 ,
,
因而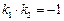 ,即
,即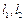 垂直.……………………………………………………16分
垂直.……………………………………………………16分
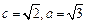 ,所以
,所以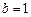 ……………………………………………2分
……………………………………………2分所以椭圆的方程为
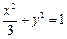 ,伴随圆的方程为
,伴随圆的方程为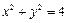 .………………4分
.………………4分(2)设直线
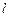 的方程
的方程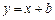 ,由
,由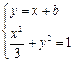 得
得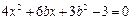
由
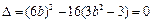 得
得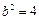 …………………………6分
…………………………6分圆心到直线
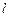 的距离为
的距离为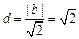 ,所以
,所以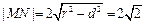 ………………………………8分
………………………………8分(3)①、当
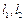 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设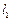 无斜率,
无斜率,因为
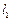 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为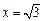 或
或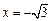 ,
,当
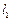 方程为
方程为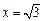 时,此时
时,此时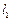 与伴随圆交于点
与伴随圆交于点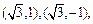
此时经过点
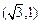 (或
(或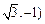 且与椭圆只有一个公共点的直线是
且与椭圆只有一个公共点的直线是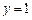 (或
(或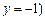 ,
,即
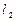 为
为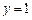 (或
(或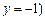 ,显然直线
,显然直线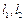 垂直;
垂直;同理可证
 方程为
方程为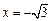 时,直线
时,直线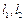 垂直.…………………………10分
垂直.…………………………10分②、当
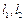 都有斜率时,设点
都有斜率时,设点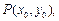 其中
其中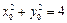 ,
,设经过点
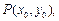 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为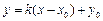 ,
,由
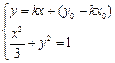 ,消去
,消去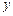 得到
得到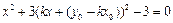 ,
,即
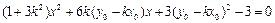 ,……………………12分
,……………………12分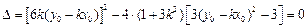 ,
,经过化简得到:
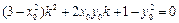 ,
, 因为
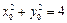 ,所以有
,所以有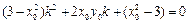 ,…………………14分
,…………………14分设
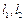 的斜率分别为
的斜率分别为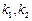 ,因为
,因为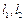 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,所以
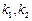 满足方程
满足方程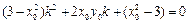 ,
,因而
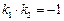 ,即
,即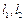 垂直.……………………………………………………16分
垂直.……………………………………………………16分略

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
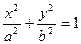
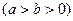 的一个顶点为
的一个顶点为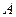
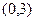 ,离心率
,离心率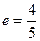
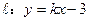 与椭圆交于不同的两点
与椭圆交于不同的两点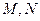 ,且满足
,且满足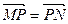 ,
,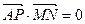 ,求直线
,求直线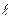 的方程.
的方程.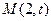
 在直线
在直线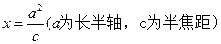 上。
上。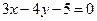 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;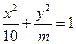 与双曲线
与双曲线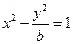 有相同的焦点,且椭圆与双曲线交于
有相同的焦点,且椭圆与双曲线交于 点
点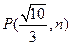 ,求椭圆及双曲线的方程.
,求椭圆及双曲线的方程.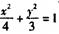 的右焦点F为圆心,并过椭圆的短轴端点的圆的方程为_
的右焦点F为圆心,并过椭圆的短轴端点的圆的方程为_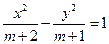 表示椭圆,则实数
表示椭圆,则实数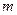 的取值范围是____________________;
的取值范围是____________________;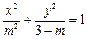 的一个焦点为
的一个焦点为 ,则
,则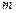 等于 .
等于 .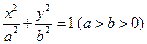 的
的 左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴, 直线AB交
左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴, 直线AB交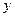 轴于点P,若
轴于点P,若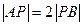 ,则椭圆的离心率是( )
,则椭圆的离心率是( )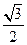

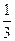
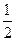
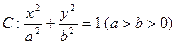 ,过右焦点
,过右焦点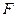 斜率为
斜率为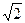 的直线与椭圆
的直线与椭圆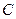 交于
交于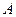 、
、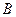 两
两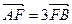 ,则椭圆
,则椭圆