题目内容
若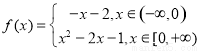 ,x1<x2<x3,且f (x1)=f (x2)=f (x3),则x1+x2+x3的值的范围是( )
,x1<x2<x3,且f (x1)=f (x2)=f (x3),则x1+x2+x3的值的范围是( )
A.[1, 2) B.(1, 2] C.(0, 1] D.[2, 3)
A.
【解析】
试题分析:由于
当x<0时,y>-2;
当x≥0时,y=(x-1)2-2≥-2,
f(0)=f(2)=-1,
由x1<x2<x3,且f (x1)=f (x2)=f (x3),
则x2+x3=2,即有x1+x2+x3=x1+2,
当f(x1)=-1即-x1-2=-1,解得x1=-1,
由-1≤x1<0,
可得1≤x1+2<2,即1≤x1+ x2+x3<2,
故选:A.

考点:分段函数的应用,二次函数的单调性.
考点分析: 考点1:函数与方程 考点2:分段函数 考点3:函数的单调性 考点4:函数的周期性 考点5:函数图像的对称性 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, ,
, ,若
,若 ,
, ,则
,则 的最大值是
的最大值是 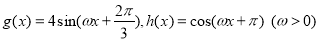 .
. 时,把
时,把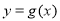 的图像向右平移
的图像向右平移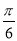 个单位得到函数
个单位得到函数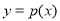 的图像,求函数
的图像,求函数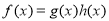 ,若
,若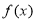 的图象与直线
的图象与直线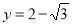 的相邻两个交点之间的距离为π,求
的相邻两个交点之间的距离为π,求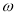 的值,并求函数
的值,并求函数 为奇函数,且当x>0时,,
为奇函数,且当x>0时,, 则
则 ( )
( )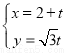 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为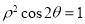 .
. [-2, 2],则输出的s属于( )
[-2, 2],则输出的s属于( )
 的离心率为
的离心率为 ,且过点
,且过点 .
.

 的焦距为
的焦距为 ,点
,点 在
在 的渐近线上,则
的渐近线上,则 的方程为( )
的方程为( )
 B.
B.


 D.
D.