题目内容
(本题满分16分)
设函数![]() 与
与![]() 的图象分别交直线
的图象分别交直线![]() 于点A,B,且曲线
于点A,B,且曲线![]() 在点A处的切线与曲线
在点A处的切线与曲线![]() 在点B处的切线平行。
在点B处的切线平行。
(1)求函数![]() 的表达式;
的表达式;
(2)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(3)当![]() 时,不等式
时,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围。
的取值范围。
(1)由![]() ,得
,得![]() ,…………………………2分
,…………………………2分
由![]() ,得
,得![]() .又由题意可得
.又由题意可得![]() ,
,
即![]() ,故
,故![]() ,或
,或![]() .………………………………4分
.………………………………4分
所以当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() .
.
由于两函数的图象都过点![]() ,因此两条切线重合,不合题意,故舍去
,因此两条切线重合,不合题意,故舍去
∴所求的两函数为![]() ,
,![]() ……………………6分
……………………6分
(2)当![]() 时,
时,![]() ,得
,得
![]()
![]() ,………………………8分
,………………………8分
由![]() ,得
,得![]() ,
,
故当![]() 时,
时,![]() ,
,![]() 递减,
递减,
当![]() 时,
时,![]() ,
,![]() 递增,
递增,
所以函数![]() 的最小值为
的最小值为![]() .…………………10分
.…………………10分
(3)![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时, ![]() ,
,![]()
![]() ,
,
![]() 在
在![]() 上为减函数,
上为减函数,![]() ,…………12分
,…………12分
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数, ![]() ,且
,且![]() .14分
.14分
要使不等式![]() 在
在![]() 上恒成立,当
上恒成立,当![]() 时,
时,![]() 为任意实数;
为任意实数;
当![]() 时,
时,![]() ,而
,而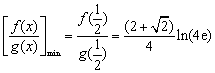 .
.
所以![]() .………………………………………………16分
.………………………………………………16分

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在