题目内容
△ABC中A,B,C的对边分别为a,b,c,且sin(B+C)+2sinA•cosB=0求:(1)角B的大小;
(2)若
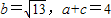 ,求△ABC的面积.
,求△ABC的面积.
【答案】分析:(1)由三角形内角和定理和诱导公式,化简已知等式得到sinA(1+2cosB)=0,结合sinA>0,可得cosB=- ,从而得到B=
,从而得到B=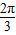 .△ABC的面积.
.△ABC的面积.
(2)根据余弦定理b2=a2+c2-2accosB的式子,结合题中数据算出ac=3,再由正弦定理的面积公式即可算出△ABC的面积.
解答:解:(1)∵B+C=π-A,∴sin(B+C)=sinA
由此可得sinA+2sinA•cosB=0,即sinA(1+2cosB)=0
∵sinA>0,∴1+2cosB=0,可得cosB=-
∵B∈(0,π),∴B=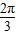 .
.
(2)∵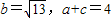 ,
,
∴根据余弦定理,得b2=a2+c2-2accos120°,
可得13=(a+c)2-ac=16-ac,解得ac=3
因此,△ABC的面积S= acsinB=
acsinB=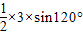 =
=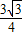 .
.
点评:本题给出三角函数等式,求解三角形ABC并求它的面积.着重考查了特殊角的三角函数值、正余弦定理解三角形和三角形面积公式等知识,属于中档题.
 ,从而得到B=
,从而得到B=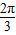 .△ABC的面积.
.△ABC的面积.(2)根据余弦定理b2=a2+c2-2accosB的式子,结合题中数据算出ac=3,再由正弦定理的面积公式即可算出△ABC的面积.
解答:解:(1)∵B+C=π-A,∴sin(B+C)=sinA
由此可得sinA+2sinA•cosB=0,即sinA(1+2cosB)=0
∵sinA>0,∴1+2cosB=0,可得cosB=-

∵B∈(0,π),∴B=
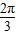 .
.(2)∵
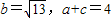 ,
,∴根据余弦定理,得b2=a2+c2-2accos120°,
可得13=(a+c)2-ac=16-ac,解得ac=3
因此,△ABC的面积S=
 acsinB=
acsinB=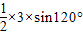 =
=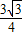 .
.点评:本题给出三角函数等式,求解三角形ABC并求它的面积.着重考查了特殊角的三角函数值、正余弦定理解三角形和三角形面积公式等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目