题目内容
(2013•延庆县一模)已知f(x)=
sin2x-2sin2x.
(Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)若x∈[0,
],求f(x)的最小值及取得最小值时对应的x的取值.
| 3 |
(Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)若x∈[0,
| π |
| 6 |
分析:(Ⅰ)利用两角和差的正弦公式化简函数的解析式为2sin(2x+
)-1,由此可得它的周期.令-
+2kπ≤2x+
≤
+2kπ(k∈Z),求得x的范围,即可求得函数的增区间.
(Ⅱ)根据x∈[0,
],利用正弦函数的定义域和值域、单调性求得f(x)的最小值及取得最小值时对应的x的取值.
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(Ⅱ)根据x∈[0,
| π |
| 6 |
解答:解:(Ⅰ)f(x)=
sin2x+cos2x-1=2sin(2x+
)-1,…(4分)
∵T=
=π,∴f(x)最小正周期为π.…(5分)
由-
+2kπ≤2x+
≤
+2kπ(k∈Z),得 …(6分)
-
+2kπ≤2x≤
+2kπ,…(7分)
-
+kπ≤x≤
+kπ,…(8分)
∴f(x)单调递增区间为[-
+kπ,
+kπ](k∈Z).…(9分)
(Ⅱ)当x∈[0,
]时,2x+
∈[
,
],…(10分)
∴f(x)在区间[0,
]单调递增,…(11分)
∴[f(x)]min=f(0)=0,对应的x的取值为0.…(13分)
| 3 |
| π |
| 6 |
∵T=
| 2π |
| 2 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
-
| 2π |
| 3 |
| π |
| 3 |
-
| π |
| 3 |
| π |
| 6 |
∴f(x)单调递增区间为[-
| π |
| 3 |
| π |
| 6 |
(Ⅱ)当x∈[0,
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
∴f(x)在区间[0,
| π |
| 6 |
∴[f(x)]min=f(0)=0,对应的x的取值为0.…(13分)
点评:本题主要考查两角和差的正弦公式,正弦函数的单调性、周期性,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
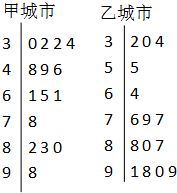 (2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
(2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重: (2013•延庆县一模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.
(2013•延庆县一模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.