题目内容
在正方体内任取一点,则该点在正方体的内切球内的概率为( )A.
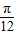
B.
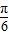
C.
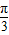
D.
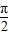
【答案】分析:根据题意,求出正方体的体积,进而可得其内切球的直径,可得其内切球的体积,由几何概型的公式,计算可得答案.
解答:解:不妨设正方体棱长为2,根据题意,棱长为2的正方体,其体积为8,
而其内切球的直径就是正方体的棱长,所以球的半径为1,
则这一点在球内的概率为: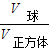 =
=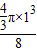 =
=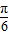 ;
;
故选B.
点评:本题考查几何概型的应用,解题的关键在于根据正方体及其内切球的位置关系,找到其内切球的直径半径,进而得到体积.
解答:解:不妨设正方体棱长为2,根据题意,棱长为2的正方体,其体积为8,
而其内切球的直径就是正方体的棱长,所以球的半径为1,
则这一点在球内的概率为:
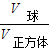 =
=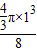 =
=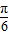 ;
;故选B.
点评:本题考查几何概型的应用,解题的关键在于根据正方体及其内切球的位置关系,找到其内切球的直径半径,进而得到体积.

练习册系列答案
相关题目