题目内容
已知:F1,F2为 的左右焦点,点A为椭圆的右顶点,直线y=x与椭圆交于B、C两点(C在第一象限),
的左右焦点,点A为椭圆的右顶点,直线y=x与椭圆交于B、C两点(C在第一象限), ,
, .
.(1)求此椭圆的方程.
(2)若P、Q是椭圆上的两点,并且满足
 ,求证:向量
,求证:向量 与
与 共线.
共线.
【答案】分析:(1)设|AC|=m,|BC|=2m,根据 ,
, ,计算|AC|,利用△COA是等腰直角三角形,可得a2=4,C(1,1)代入
,计算|AC|,利用△COA是等腰直角三角形,可得a2=4,C(1,1)代入 ,可得
,可得 ,从而可求椭圆的方程;
,从而可求椭圆的方程;
(2)设直线PC的斜率为k,则直线QC的斜率为-k,由 得(3k2+1)x2-6k(k-1)x+3k2-6k-1=0,从而可求PQ的斜率,利用
得(3k2+1)x2-6k(k-1)x+3k2-6k-1=0,从而可求PQ的斜率,利用 ,所以PQ与AB平行,所以
,所以PQ与AB平行,所以 与
与 共线.
共线.
解答:(1)解:设|AC|=m,|BC|=2m
∵ ,
, ,
,
∴m2+4m2=10
∴
∵△COA是等腰直角三角形
∴a2=4,C(1,1)
代入 ,可得
,可得
∴椭圆的方程为
(2)证明:设直线PC的斜率为k,则直线QC的斜率为-k,
由 得(3k2+1)x2-6k(k-1)x+3k2-6k-1=0
得(3k2+1)x2-6k(k-1)x+3k2-6k-1=0
∴ ,
,
∴ ,
,
同理 ,
,
∴
而 ,所以PQ与AB平行,所以
,所以PQ与AB平行,所以 与
与 共线.
共线.
点评:本题以向量为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.
 ,
, ,计算|AC|,利用△COA是等腰直角三角形,可得a2=4,C(1,1)代入
,计算|AC|,利用△COA是等腰直角三角形,可得a2=4,C(1,1)代入 ,可得
,可得 ,从而可求椭圆的方程;
,从而可求椭圆的方程;(2)设直线PC的斜率为k,则直线QC的斜率为-k,由
 得(3k2+1)x2-6k(k-1)x+3k2-6k-1=0,从而可求PQ的斜率,利用
得(3k2+1)x2-6k(k-1)x+3k2-6k-1=0,从而可求PQ的斜率,利用 ,所以PQ与AB平行,所以
,所以PQ与AB平行,所以 与
与 共线.
共线.解答:(1)解:设|AC|=m,|BC|=2m
∵
 ,
, ,
,∴m2+4m2=10
∴

∵△COA是等腰直角三角形
∴a2=4,C(1,1)
代入
 ,可得
,可得
∴椭圆的方程为

(2)证明:设直线PC的斜率为k,则直线QC的斜率为-k,
由
 得(3k2+1)x2-6k(k-1)x+3k2-6k-1=0
得(3k2+1)x2-6k(k-1)x+3k2-6k-1=0∴
 ,
,∴
 ,
,同理
 ,
,∴

而
 ,所以PQ与AB平行,所以
,所以PQ与AB平行,所以 与
与 共线.
共线.点评:本题以向量为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左右焦点,点A为椭圆的右顶点,直线y=x与椭圆交于B、C两点(C在第一象限),
的左右焦点,点A为椭圆的右顶点,直线y=x与椭圆交于B、C两点(C在第一象限),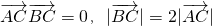 ,
,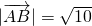 .
.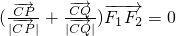 ,求证:向量
,求证:向量 与
与 共线.
共线.