题目内容
给出方程:(
)x+xlnx-1=0,下列命题如下:
①该方程有小于零的实数解;
②该方程有无数个实数解;
③方程有且只有一个实数解;
④有x0为方程的实数解,则x0>-1;
则正确的命题是 .
| 1 | 2 |
①该方程有小于零的实数解;
②该方程有无数个实数解;
③方程有且只有一个实数解;
④有x0为方程的实数解,则x0>-1;
则正确的命题是
分析:在同一坐标系中画出函数y=(
)x与y=1-xlnx的图象,分析图象交点的个数及交点横坐标的值,进而根据方程根与对应函数图象交点的关系,进而判断出四个结论的真假,可得答案.
| 1 |
| 2 |
解答:解:若x<0,则(
)x+xlnx-1=0无意义,
故该方程无小于零的实数解,故①错误;
若(
)x+xlnx-1=0,则(
)x=1-xlnx
令y=1-xlnx,则y′=-1-lnx,令y′=0,则x=
当x∈(0,
)时,y′>0,此时y=1-xlnx为增函数,
当x∈(
,+∞)时,y′<0,此时y=1-xlnx为减函数,
∴函数y=(
)x与y=1-xlnx的图象如下图所示:
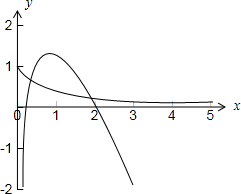
由图可知:函数y=(
)x与y=1-xlnx的图象有两个交点,交点横坐标均大于-1
故②③错误,④正确;
故答案为:④
| 1 |
| 2 |
故该方程无小于零的实数解,故①错误;
若(
| 1 |
| 2 |
| 1 |
| 2 |
令y=1-xlnx,则y′=-1-lnx,令y′=0,则x=
| 1 |
| e |
当x∈(0,
| 1 |
| e |
当x∈(
| 1 |
| e |
∴函数y=(
| 1 |
| 2 |
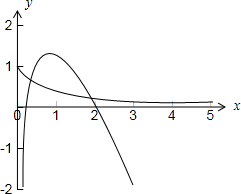
由图可知:函数y=(
| 1 |
| 2 |
故②③错误,④正确;
故答案为:④
点评:本题以命题的真假判断为载体考查了函数的零点与方程的根,熟练掌握图象法求函数零点的方法和步骤是解答的关键.

练习册系列答案
相关题目
