题目内容
已知平面向量
=（
，-1），
=（
，
）．
（I）若存在实数k和t，使得
=+（t2-3），
=-k+，且
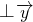，试求函数的关系式k=f（t）；
（II）根据（I）结论，确定k=f（t）的单调区间．
解：（I）∵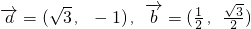
∴
∴
∵
，∴
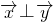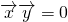
即
，
∴t3-3t-4k=0
即k=
（II）由（I）知，k=f（t）=，
∴
令k′＜0得-1＜t＜1，令k′＞0得t＜0或t＞1
故k=f（t）的单调递减区间是[-1，1]；
单调递增区间是（-∞，-1]，[1，+∞）．
分析：（I）利用向量模的坐标公式求出向量的模，利用向量垂直的充要条件列出方程，将方程变形表示出k．
（II）求出函数f（t）的导数，令导数大于0，求出不等式的解集即为单调递增区间；令导函数小于0求出不等式的解集为单调递减区间．
点评：本题考查向量模的坐标公式；向量垂直的充要条件；利用导数求函数的单调区间．
∴
∴
∵
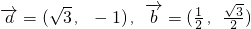
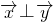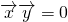
，∴即
，∴t3-3t-4k=0
即k=
（II）由（I）知，k=f（t）=
，∴
令k′＜0得-1＜t＜1，令k′＞0得t＜0或t＞1
故k=f（t）的单调递减区间是[-1，1]；
单调递增区间是（-∞，-1]，[1，+∞）．
分析：（I）利用向量模的坐标公式求出向量的模，利用向量垂直的充要条件列出方程，将方程变形表示出k．
（II）求出函数f（t）的导数，令导数大于0，求出不等式的解集即为单调递增区间；令导函数小于0求出不等式的解集为单调递减区间．
点评：本题考查向量模的坐标公式；向量垂直的充要条件；利用导数求函数的单调区间．
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
已知平面向量
=（1，-3），
=（4，-2），λ
+
与
垂直，则λ是（ ）
| a |
| b |
| a |
| b |
| a |
| A、-1 | B、1 | C、-2 | D、2 |
已知平面向量
，
满足|
|=1，|
|=2，
与
的夹角为60°，则“m=1”是“(
-m
)⊥
”的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |