题目内容
如图所示,等腰梯形的两底分别为AD=2a,BC=a,∠BAD=45°,直线MN⊥AD,交AD于M,交折线ABCD于N,设AM=x,试将梯形ABCD位于直线MN左侧的面积y表示成x的函数,并求此函数的定义域.
解：过B、C分别作边AD的垂线,垂足分别为H和G,则AH=
,AG=
a,当M位于H左侧时,AM=x,MN=x.故y=S△AMN=
x2(0≤x<
);
当M位于H、G之间时,y=S梯形ABNM=
(AM+BN)·MN=
(x+x-
)·
=
ax-
a2(
≤x<
);
当M位于G、D之间时,y=S梯形ABCD-S△DMN=
·
·-
(2a-x)2=-
x2+2ax-
a2(
≤x≤2a).
故y=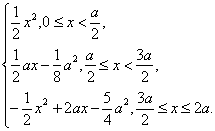
其定义域为［0,2a］,值域为［0,
a2］.
练习册系列答案
智能训练练测考系列答案
相关题目
已知几何体A-BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．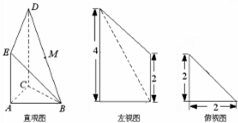
（2012•上饶一模）如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图，在直观图中，M是BD的中点，左视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．
如图所示，直观图四边形A′B′C′D′是一个底角为45°的等腰梯形，那么原平面图形是（ ）| A、任意梯形 | B、直角梯形 | C、任意四边形 | D、平行四边形 |
