题目内容
a是实数,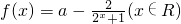 ,用定义证明:对于任意a,f(x)在R上为增函数.
,用定义证明:对于任意a,f(x)在R上为增函数.
证明:设x1,x2∈R,x1<x2,则
f(x1)-f(x2)= -------------(2分)
-------------(2分)
=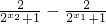 =
=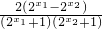 ,-----------------(4分)
,-----------------(4分)
∵指数函数y=2x在R上是增函数,且x1<x2,
∴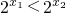 ,可得
,可得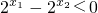 ,---------------------(6分)
,---------------------(6分)
又∵2x>0,得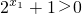 ,
,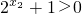 ,--------------(8分)
,--------------(8分)
∴f(x1)-f(x2)<0即f(x1)<f(x2),
由此可得,对于任意a,f(x)在R上为增函数.----------(10分)
分析:设两个实数数x1、x2∈R,且x1<x2,将f(x1)与f(x2)作差变形整理,再讨论得f(x1)<f(x2),由此即可得到 在区间(0,2)上为减函数.
在区间(0,2)上为减函数.
点评:本题通过证明一个函数在给定区间上为增函数,考查了用定义证明函数单调性的知识,属于基础题.
f(x1)-f(x2)=
 -------------(2分)
-------------(2分)=
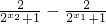 =
=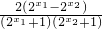 ,-----------------(4分)
,-----------------(4分)∵指数函数y=2x在R上是增函数,且x1<x2,
∴
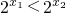 ,可得
,可得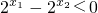 ,---------------------(6分)
,---------------------(6分)又∵2x>0,得
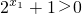 ,
,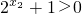 ,--------------(8分)
,--------------(8分)∴f(x1)-f(x2)<0即f(x1)<f(x2),
由此可得,对于任意a,f(x)在R上为增函数.----------(10分)
分析:设两个实数数x1、x2∈R,且x1<x2,将f(x1)与f(x2)作差变形整理,再讨论得f(x1)<f(x2),由此即可得到
 在区间(0,2)上为减函数.
在区间(0,2)上为减函数.点评:本题通过证明一个函数在给定区间上为增函数,考查了用定义证明函数单调性的知识,属于基础题.

练习册系列答案
相关题目
 ,用定义证明:对于任意a,f(x)在R上为增函数.
,用定义证明:对于任意a,f(x)在R上为增函数. ,用定义证明:对于任意a,f(x)在R上为增函数.
,用定义证明:对于任意a,f(x)在R上为增函数.