题目内容
某种产品每件成本为6元,每件售价为x元(6<x<11),年销售为u万件,若已知 -u与
-u与 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(Ⅰ)求年销售利润y关于售价x的函数关系式;
(Ⅱ)求售价为多少时,年利润最大,并求出最大年利润.
解:(Ⅰ)设 -u=k
-u=k , 1分
, 1分
∵售价为10元时,年销量为28万件,∴ -28=k
-28=k ,解得k=2. 3分
,解得k=2. 3分
∴u=-2 +
+ =-2x2+21x+18. 4分
=-2x2+21x+18. 4分
∴y=(-2x2+21x+18)(x-6)=-2x3+33x2-108x-108(6<x<11). 6分
(Ⅱ)y′=-6x2+66x-108=-6(x2-11x+18)=-6(x-2)(x-9). 7分
令y′=0,得x=2(舍去)或x=9, 8分
当x∈(6,9)时,y′>0;当x∈(9,11)时,y′<0. 9分
∴函数y=-2x3+33x2-108x-108在(6,9)上是递增的,在(9,11)上是递减的. 10分
∴当x=9时,y取最大值,且ymax=135, 11分
∴售价为9元时,年利润最大,最大年利润为135万元. 12分

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
设ξ的分布列如右,则x等于( )
A.0 B. C.
C. D.
D.
| ξ | -1 | 0 | 1 |
| Pi |
|
| x |
 (B)最长棱的棱长为
(B)最长棱的棱长为

 间的距离等于4,则该双曲线方程是___________.
间的距离等于4,则该双曲线方程是___________. , 则
, 则 的值为( ).
的值为( ). B.
B. C.
C. D.
D.
 ,且
,且 ,则
,则
 为实数,则下列命题正确的是( )
为实数,则下列命题正确的是( ) ,则
,则 B.若
B.若 ,
,
 D.若
D.若
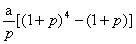 D.
D. 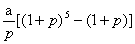
 ,公差
,公差 ,则使前
,则使前 项和
项和 取最大值的正整数
取最大值的正整数
