题目内容
【题目】如图1 ,在△ABC中,AB=BC=2, ∠B=90°,D为BC边上一点,以边AC为对角线做平行四边形ADCE,沿AC将△ACE折起,使得平面ACE ⊥平面ABC,如图2.
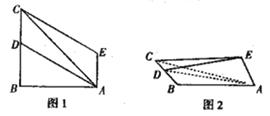
(1)在图 2中,设M为AC的中点,求证:BM丄AE;
(2)在图2中,当DE最小时,求二面角A -DE-C的平面角.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)根据题设条件推出![]() ,再由平面
,再由平面![]() 平面
平面![]() 推出
推出![]() 平面
平面![]() ,即可得证;(2)分别以射线
,即可得证;(2)分别以射线![]() ,
, ![]() 的方向为
的方向为![]() ,
, ![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,求出当
,求出当![]() 最小时,点
最小时,点![]() 和
和![]() 的坐标,分别求出平面
的坐标,分别求出平面![]() 和平面
和平面![]() 的法向量,代入向量夹角公式,可得二面角
的法向量,代入向量夹角公式,可得二面角![]() 的平面角.
的平面角.
试题解析:(1)证明:∵在![]() 中,
中, ![]() ,
, ![]()
∴当![]() 为
为![]() 的中点时,
的中点时, ![]()
∵平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
∴![]() 平面
平面![]()
∵![]() 平面
平面![]()
∴![]()
(2)如图,分别以射线![]() ,
, ![]() 的方向为
的方向为![]() ,
, ![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]()
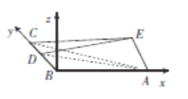
设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]()
∵![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]()
∴![]()
∴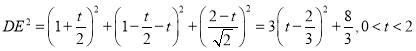
当且仅当![]() 时,
时, ![]() 最小,此时
最小,此时![]() ,
, 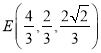
设![]() ,
, ![]() 平面
平面![]() ,则
,则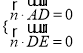 ,即
,即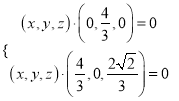
∴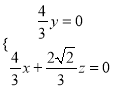
令![]() ,可得
,可得![]() ,
, ![]() ,则有
,则有![]()
∴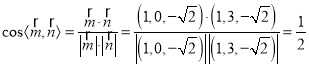
∴观察可得二面角![]() 的平面角
的平面角![]()

练习册系列答案
相关题目
