题目内容
(本小题满分12分)参加市数学调研抽测的某高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:

(Ⅰ)求参加数学抽测的人数 、抽测成绩的中位数及分数分别在
、抽测成绩的中位数及分数分别在 ,
, 内的人数;
内的人数;
(Ⅱ)若从分数在 内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在 内的概率.
内的概率.
(Ⅰ) ,中位数为73,分数在
,中位数为73,分数在 、
、 内的人数分别为
内的人数分别为 人、
人、 人.
人.
(Ⅱ)
【解析】
试题分析:(Ⅰ)茎叶图保留了原始数据很容易知道分数在分数在 内的频数为2,由频率分布直方图可以看出,分数在
内的频数为2,由频率分布直方图可以看出,分数在 内同样有
内同样有 人.
人.  , 得
, 得 茎叶图可知抽测成绩的中位数为73,通过计算可得成绩在
茎叶图可知抽测成绩的中位数为73,通过计算可得成绩在 内的人数、(2)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(3)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;(4)在频率分布直方图,小长方形的面积是表示数据落在小组内的频率,它的高是频率与组距的比;
内的人数、(2)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(3)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;(4)在频率分布直方图,小长方形的面积是表示数据落在小组内的频率,它的高是频率与组距的比;
试题解析:(Ⅰ)分数在 内的频数为2,由频率分布直方图可以看出,分数在
内的频数为2,由频率分布直方图可以看出,分数在 内同样有
内同样有 人. 2分,
人. 2分,
由 , 得
, 得 , 3分
, 3分
茎叶图可知抽测成绩的中位数为 . 4分
. 4分
 分数在
分数在 之间的人数为
之间的人数为 5分
5分
参加数学竞赛人数 ,中位数为73,分数在
,中位数为73,分数在 、
、 内的人数分别为
内的人数分别为 人、
人、 人. 6分
人. 6分
(Ⅱ)设“在 内的学生中任选两人,恰好有一人分数在
内的学生中任选两人,恰好有一人分数在 内”为事件
内”为事件 ,
,
将 内的
内的 人编号为
人编号为 ;
; 内的
内的 人编号为
人编号为 ,
,
在 内的任取两人的基本事件为:
内的任取两人的基本事件为:


 共15个, 9分
共15个, 9分
其中,恰好有一人分数在 内的基本事件有
内的基本事件有



 共8个,故所求的概率得
共8个,故所求的概率得 , 11分
, 11分
答:恰好有一人分数在 内的概率为
内的概率为 . 12
. 12
考点:茎叶图及频率分布直方图 及概率问题

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
 与双曲线
与双曲线
 的焦点重合,且双曲线
的焦点重合,且双曲线 的渐近线为
的渐近线为 ,则双曲线
,则双曲线 的实轴长为( )
的实轴长为( ) B.
B. C.
C. D.
D.
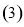 班共有学生
班共有学生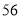 人,现根据座号,用系统抽样的方法,抽取一个容量为
人,现根据座号,用系统抽样的方法,抽取一个容量为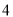 的样本.已知
的样本.已知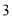 号、
号、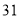 号、
号、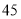 号同学在样本中,那么样本中还有一个同学的座号是( )
号同学在样本中,那么样本中还有一个同学的座号是( )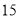 B.
B.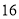 C.
C.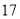 D.
D.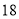
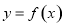 (
(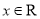 )满足
)满足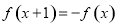 ,且
,且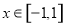 时,
时,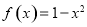 ,已知函数
,已知函数 ,则函数
,则函数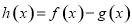 在区间
在区间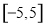 内的零点的个数为( )
内的零点的个数为( )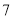 B.
B.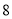 C.
C.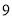 D.
D.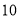
 ,集合
,集合 ,
, ,则集合
,则集合 ( )
( ) B.
B. C.
C. D.
D.
 满足
满足 的取值范围为____________
的取值范围为____________ 中,内角A,B,C所对的边长分别为
中,内角A,B,C所对的边长分别为

 B.
B. C.
C. D.
D.
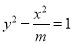 的离心率
的离心率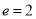 ,则以双曲线的两条渐近线与抛物线
,则以双曲线的两条渐近线与抛物线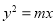 的交点为顶点的三角形的面积为
的交点为顶点的三角形的面积为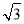 B.
B. C.
C.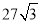 D.
D.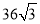
 的单调递增区间为 .
的单调递增区间为 .