题目内容
函数f（x）=sinx（sinx-cosx）的最小正周期为 ．
【答案】分析：利用两角和的正弦公式，二倍角公式，把函数f（x）化为Asin（ωx+φ）+B的形式，最后利用周期公式解之即可．
解答：解：函数f（x）=sinx（sinx-cosx）=sin2x-sinxcosx=-
sin2x-
cos2x+
=-
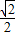sin（2x+
）+
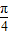，故它的最小正周期等于
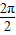=π，
故答案为：π．
点评：本题主要考查两角和的正弦公式，二倍角公式，正弦函数的周期性，同时考查了运算求解的能力，属于基础题．
解答：解：函数f（x）=sinx（sinx-cosx）=sin2x-sinxcosx=-
sin2x-cos2x+=-
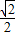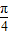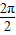sin（2x+）+，故它的最小正周期等于=π，故答案为：π．
点评：本题主要考查两角和的正弦公式，二倍角公式，正弦函数的周期性，同时考查了运算求解的能力，属于基础题．
练习册系列答案
相关题目
函数f（x）=sin（ωx+?）（x∈R，ω＞0，0≤?＜2π）的部分图象如图，则