题目内容
【题目】如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点. 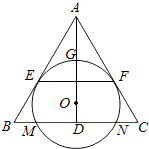
(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=2 ![]() ,求四边形EBCF的面积.
,求四边形EBCF的面积.
【答案】
(1)证明:∵△ABC为等腰三角形,AD⊥BC,
∴AD是∠CAB的角平分线,
又∵圆O分别与AB、AC相切于点E、F,
∴AE=AF,∴AD⊥EF,
∴EF∥BC
(2)解:由(1)知AE=AF,AD⊥EF,∴AD是EF的垂直平分线,
又∵EF为圆O的弦,∴O在AD上,
连结OE、OM,则OE⊥AE,
由AG等于圆O的半径可得AO=2OE,
∴∠OAE=30°,∴△ABC与△AEF都是等边三角形,
∵AE=2 ![]() ,∴AO=4,OE=2,
,∴AO=4,OE=2,
∵OM=OE=2,DM= ![]() MN=
MN= ![]() ,∴OD=1,
,∴OD=1,
∴AD=5,AB= ![]() ,
,
∴四边形EBCF的面积为 ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.

【解析】(1)通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F,利用相似的性质即得结论;(2)通过(1)知AD是EF的垂直平分线,连结OE、OM,则OE⊥AE,利用S△ABC﹣S△AEF计算即可.

【题目】某奶茶店为了解白天平均气温与某种饮料销量之间的关系进行分析研究,记录了2月21日至2月25日
的白天平均气温x(℃)与该奶茶店的这种饮料销量y(杯),得到如表数据:
平均气温x(℃) | 9 | 11 | 12 | 10 | 8 |
销量y(杯) | 23 | 26 | 30 | 25 | 21 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)试根据(1)求出的线性回归方程,预测平均气温约为20℃时该奶茶店的这种饮料销量.
(参考: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ;9×23+11×26+12×30+10×25+8×21=1271,92+112+122+102+82=510)
;9×23+11×26+12×30+10×25+8×21=1271,92+112+122+102+82=510)
【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
累计净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共![]() 台,其累计净化量都分布在区间
台,其累计净化量都分布在区间![]() 内,为了解其质量,随机抽取了
内,为了解其质量,随机抽取了![]() 台净化器作为样本进行估计,按照
台净化器作为样本进行估计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均匀分组,其中累计净化量在
均匀分组,其中累计净化量在![]() 的所有数据有:
的所有数据有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并绘制了如下频率分布直方图.
,并绘制了如下频率分布直方图.
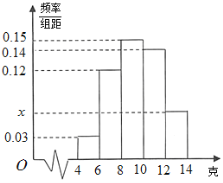
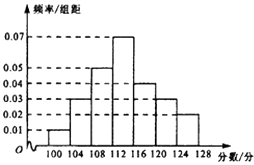
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累计净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.