Question

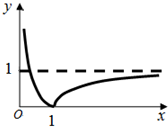函数g（x）（x∈R）的图象如图所示，关于x的方程[g（x）]²+m•g（x）+2m+3=0有三个不同的实数解，则m的取值范围是

 

．

Answer 1

分析：设g（x）=t，由题意可得t²+mt+2m+3=0有两个根，且一个在（0，1）上，一个在[1，+∞）上．设h（t）=t²+mt+2m+3，①当有一个根为1时，由h（1）=0，求得m的值，检验符合题意．②当没有根为1时，由

h(0)=2m+3＞0 h(1)=1+m+2m+3＜0

，求得m的范围，综合可得答案．

解答：解：根据函数g（x）（x∈R）的图象，设g（x）=t，
∵关于x的方程[g（x）]²+m•g（x）+2m+3=0有有三个不同的实数解，
即为t²+mt+2m+3=0有两个根，且一个在（0，1）上，一个在[1，+∞）上．
设h（t）=t²+mt+2m+3，
①当有一个根为1时，h（1）=1+m+2m+3=0，m=-

4

3

，此时另一根为

1

3

符合题意．
②当没有根为1时，则：

h(0)=2m+3＞0 h(1)=1+m+2m+3＜0

，解得-

3

2

＜m＜-

4

3

．
综上可得，m的取值范围是 （-

3

2

，

4

3

]，
故答案为：（-

3

2

，

4

3

]．

点评：本题主要考查对数函数、二次函数的图象和性质综合应用，体现了分类讨论的数学思想．