题目内容
已知:p:函数g(x)=x+
,g(x)在区间(0,2]上的值不小于6;q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0},且A∩B=φ,求实数a的取值范围,使p、q中有且只有一个为真命题.
| a+1 | x |
分析:先分别求出命题p、q为真命题时的a的取值范围,进而讨论p真q假,p假q真,即可得出答案.
解答:解:若P为真时:由题意知g(x)=x+
≥6,x∈(0,2]
∴a+1≥x(6-x)即a≥-x2+6x-1,x∈(0,2],
令h(x)=-x2+6x-1,x∈(0,2].
而h(x)=-x2+6x-1=-(x-3)2+8
∴x∈(0,2]时,h(x)max=h(2)=7
∴a≥7.
若q为真时,
当△<0时,A=φ,此时(a+2)2-4<0,解得-4<a<0;
当△≥0时,A≠φ,由A∩B=φ,x1x2=1>0,得
,解得a≥0;
故a>-4.
①要使P真q假,则
,∴a不存在;
②要使P假q真,则
得-4<a<7.
∴当实数a的取值范围是(-4,7)时,p、q中有且只有一个为真命题.
| a+1 |
| x |
∴a+1≥x(6-x)即a≥-x2+6x-1,x∈(0,2],
令h(x)=-x2+6x-1,x∈(0,2].
而h(x)=-x2+6x-1=-(x-3)2+8
∴x∈(0,2]时,h(x)max=h(2)=7
∴a≥7.
若q为真时,
当△<0时,A=φ,此时(a+2)2-4<0,解得-4<a<0;
当△≥0时,A≠φ,由A∩B=φ,x1x2=1>0,得
|
故a>-4.
①要使P真q假,则
|
②要使P假q真,则
|
∴当实数a的取值范围是(-4,7)时,p、q中有且只有一个为真命题.
点评:正确求出命题p、q都为真命题时的a的取值范围和利用分类讨论的方法是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
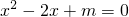 有解,则p是q的
有解,则p是q的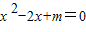 有解,则p是q的( )
有解,则p是q的( )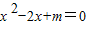 有解,则p是q的( )
有解,则p是q的( )