题目内容
【题目】若圆(x-1)2+(y+1)2=R2上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是( )
A. R>1 B. R<3 C. 1<R<3 D. R≠2
【答案】C
【解析】分析:圆(x-1)2+(y+1)2=R2上有且仅有两个点到直线4x+3y=11的距离等于1,先求圆心到直线的距离,再求半径的范围.
详解:
依题意可得,直线与圆可能相交,相切或相离.若直线4x+3y=11与圆(x-1)2+(y+1)2=R2相离,则圆上的点到直线的最小距离应小于1,即圆心到直线的距离d∈(R,1+R),从而有R<![]() <1+R,解得1<R<2.
<1+R,解得1<R<2.
若直线4x+3y=11与圆(x-1)2+(y+1)2=R2相切,则R=![]() =2.
=2.
若直线4x+3y=11与圆相交,则圆上的点到直线的最小距离应小于1,即圆心到直线的距离d∈(R-1,R),从而有R-1<![]() <R,解得2<R<3.综上可得1<R<3,故选C.
<R,解得2<R<3.综上可得1<R<3,故选C.
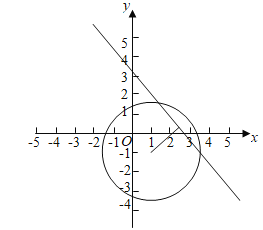

练习册系列答案
相关题目