题目内容
过抛物线y2=4x的准线与对称轴的交点作直线,交抛物线于M、N两点,问直线的倾斜角多大时,以线段MN为直径的圆经过抛物线的焦点?
解:抛物线y2=4x的准线与对称轴的交点为(-1,0).设直线MN的方程为y=k(x+1).
由![]() 得k2x2+2(k2-2)x+k2=0.
得k2x2+2(k2-2)x+k2=0.
∵直线与抛物线交于M、N两点,
∴Δ=4(k2-2)2-4k4>0,
即k2<|k2-2|,k2<1,-1<k<1.
设M(x1,y1),N(x2,y2),抛物线焦点为F(1,0).
∵以线段MN为直径的圆经过抛物线的焦点,
∴MF⊥NF.
∴![]() ·
·![]() =-1,
=-1,
即y1y2+x1x2-(x1+x2)+1=0.
又x1+x2=-![]() ,1x2=1,
,1x2=1,
y12y22=16x1x2=16且y1、y2同号,∴![]() =-6.
=-6.
解得k2=![]() .∴k=±
.∴k=±![]() ,
,
即直线的倾斜角为arctan![]() 或π-arctan
或π-arctan![]() 时,以线段MN为直径的圆经过抛物线的焦点.
时,以线段MN为直径的圆经过抛物线的焦点.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
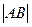 =8,求 直线l的斜率
=8,求 直线l的斜率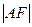 =m,
=m,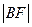 =n.求证
=n.求证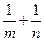 为定值
为定值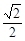 B.
B.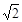 C.
C.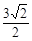 D.2
D.2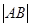 =8,求 直线l的斜率
=8,求 直线l的斜率 =m,
=m, =n.求证
=n.求证 为定值
为定值