题目内容
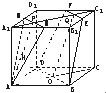 如图,在正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点,AB=a.
如图,在正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点,AB=a.(1)求证:平面AMN∥平面EFDB;
(2)求异面直线BE与MN之间的距离.
分析:(1)要证:平面AMN∥平面EFDB,证明MN∥平面EFDB.AM∥平面EFDB,即可;
(2)求异面直线BE与MN之间的距离,转化为两平行平面之间的距离.
(2)求异面直线BE与MN之间的距离,转化为两平行平面之间的距离.
解答:(1)证明:∵MN∥EF,∴MN∥平面EFDB.
又AM∥DF,
∴AM∥平面EFDB.而MN∩AM=M,
∴平面AMN∥平面EFDB.
(2)解:∵BE?平面EFDB,MN?平面AMN,且平面AMN∥平面EFDB,
∴BE与MN之间的距离等于两平行平面之间的距离.
作出这两个平面与平面A1ACC1的交线AP、OQ,作OH⊥AP于H.
∵DB⊥平面A1ACC1,
∴DB⊥OH.而MN∥DB,∴OH⊥MN.
则OH⊥平面AMN.
∵A1P=
a,AP=
a,
设∠A1AP=θ,则cosθ=
=
,
∴OH=AO•sinθ=
a•
a=
a.
∴异面直线BE与MN的距离是
a.
又AM∥DF,
∴AM∥平面EFDB.而MN∩AM=M,
∴平面AMN∥平面EFDB.
(2)解:∵BE?平面EFDB,MN?平面AMN,且平面AMN∥平面EFDB,
∴BE与MN之间的距离等于两平行平面之间的距离.
作出这两个平面与平面A1ACC1的交线AP、OQ,作OH⊥AP于H.
∵DB⊥平面A1ACC1,
∴DB⊥OH.而MN∥DB,∴OH⊥MN.
则OH⊥平面AMN.
∵A1P=
| ||
| 4 |
3
| ||
| 4 |
设∠A1AP=θ,则cosθ=
| a | ||||
|
2
| ||
| 3 |
∴OH=AO•sinθ=
| ||
| 2 |
2
| ||
| 3 |
| 2 |
| 3 |
∴异面直线BE与MN的距离是
| 2 |
| 3 |
点评:本题考查平面与平面平行,异面直线间的距离,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )