题目内容
在平面直角坐标系xoy中,曲线C1的参数方程为  (
( ,
, 为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1,
为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1, )对应的参数j=
)对应的参数j= ,曲线C2过点D(1,
,曲线C2过点D(1, ).
).
(I)求曲线C1,C2的直角坐标方程;
(II)若点A(r1,q),B(r2,q+ )在曲线C1上,求
)在曲线C1上,求 的值.
的值.
(1)曲线C1的方程为 ,曲线
,曲线 的方程为
的方程为 ;(2)
;(2) .
.
解析试题分析:本题主要考查直角坐标系与极坐标系之间的转化、参数方程与普通方程的互化,考查学生的转化能力和计算能力.第一问,利用参数方程和普通方程的互化公式得到曲线 的方程,先设出曲线
的方程,先设出曲线 的普通方程,将点
的普通方程,将点 转化为直角坐标代入所设的曲线
转化为直角坐标代入所设的曲线 的方程中,得到
的方程中,得到 的值,即得到曲线
的值,即得到曲线 的直角坐标方程;第二问,因为点
的直角坐标方程;第二问,因为点 在曲线
在曲线 上,所以代入到
上,所以代入到 的方程中,得到2个表达式,代入到所求的式子中即可.
的方程中,得到2个表达式,代入到所求的式子中即可.
试题解析:(I)将 及对应的参数
及对应的参数 ,
,
代入 ,得
,得 ,
,
即 ,
,
所以曲线C1的方程为 .
.
设圆 的半径为
的半径为 ,由题意圆
,由题意圆 的方程为
的方程为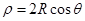 ,(或
,(或 ).
).
将点 代入
代入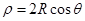 ,得
,得 ,即
,即 ,
,
(或由 ,得
,得 ,代入
,代入 ,得
,得 ),
),
所以曲线 的方程为
的方程为 ,或
,或 .
.
(Ⅱ)因为点 ,
, 在曲线
在曲线 上,
上,
所以 ,
, ,
,
所以 .
.
考点:1.参数方程与普通方程的互化;2.极坐标与直角坐标的互化.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 的参数方程为
的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (
( 为参数).
为参数). ,判断点P与直线
,判断点P与直线 ,方向向量为
,方向向量为 的直线,圆方程
的直线,圆方程
 两点,求
两点,求 的值
的值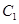 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
. ).
). 中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为
中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为 ,M,N分别为C与x轴,y轴的交点.
,M,N分别为C与x轴,y轴的交点. 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 .试求曲线
.试求曲线 内,直线
内,直线 的参数方程为
的参数方程为
 为参数
为参数 .以
.以 为极轴建立极坐标系,圆
为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .判断直线
.判断直线 =2
=2 .
. (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.