题目内容
10.下列计算错误的是( )| A. | $\int_{-π}^π$sinxdx=0 | B. | $\int_0^1$${\sqrt{x}$dx=$\frac{2}{3}}$ | ||
| C. | $\int_{-\frac{π}{2}}^{\frac{π}{2}}$cosxdx=2$\int_0^{\frac{π}{2}}$cosxdx | D. | $\int_{-1}^1$x2dx=0 |
分析 利用定积分化简求解即可.
解答 解:$\int_{-π}^π$sinxdx=-cosx${|}_{-\frac{π}{2}}^{\frac{π}{2}}$=0,所以A正确.
$\int_0^1$${\sqrt{x}$dx=$\frac{2}{3}{x}^{\frac{3}{2}}{|}_{0}^{1}$=$\frac{2}{3}$,所以B正确.
$\int_{-\frac{π}{2}}^{\frac{π}{2}}$cosxdx=2$\int_0^{\frac{π}{2}}$cosxdx,满足定积分的运算法则,正确;
$\int_{-1}^1$x2dx=$\frac{1}{3}{x}^{3}$${|}_{-1}^{1}$=$\frac{2}{3}$,所以D不正确;
故选:D.
点评 本题考查定积分的应用,考查计算能力.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
20.在△ABC中,内角A、B、C所对的边分别为a、b、c,且$\frac{2a+b}{c}$=$\frac{cos(A+C)}{cosC}$,c=2,则△ABC面积的最大值为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $2\sqrt{3}$ |
1.某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如表:
(Ⅰ)试根据上述数据,求这个班级女生阅读名著的平均本数;
(Ⅱ)若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率.
| 阅读名著的本数 | 1 | 2 | 3 | 4 | 5 |
| 男生人数 | 3 | 1 | 2 | 1 | 3 |
| 女生人数 | 1 | 3 | 3 | 1 | 2 |
(Ⅱ)若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率.
18.设集合A={x|(x-1)(x-2)2=0},则集合A中元素的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.函数f(x)=x3-3x在[-3,$\frac{3}{2}$]上的最大值和最小值分别是( )
| A. | 2,-2 | B. | 2,-18 | C. | 18,-2 | D. | 18,-18 |
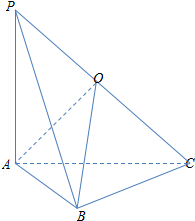 如图,已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,且AB=BC=1,PA=$\sqrt{2}$,O为线段PC的中点,
如图,已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,且AB=BC=1,PA=$\sqrt{2}$,O为线段PC的中点,