题目内容
已知函数:f(x)=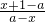 (a∈R且x≠a).
(a∈R且x≠a).
(1)证明:f(x)+f(2a-x)+2=0对定义域内的所有x都成立;
(2)当f(x)的定义域为[a+ ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(3)若a> ,函数g(x)=x2+|(x-a) f(x)|,求g(x)的最小值.
,函数g(x)=x2+|(x-a) f(x)|,求g(x)的最小值.
(1)证明:∵f(x)=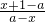 =
= -1,
-1,
∴f(2a-x)= -1=-
-1=- -1,
-1,
∴f(x)+f(2a-x)+2= +(-
+(- )-2+2=0,与x取值无关.
)-2+2=0,与x取值无关.
∴f(x)+f(2a-x)+2=0对定义域内的所有x都成立;
(2)证明:∵f(x)的定义域为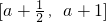 ,
,
∴-1-a≤-x≤-a- ,-1≤a-x≤-
,-1≤a-x≤- ,-2≤
,-2≤ ≤-1,
≤-1,
又f(x)= -1,
-1,
∴-3≤ -1≤-2,即f(x)的值域为[-3,-2].
-1≤-2,即f(x)的值域为[-3,-2].
(3)解:函数g(x)=x2+|x+1-a|,(x≠a),
①当x≥a-1且x≠a时,g(x)=x2+x+1-a=(x+ )2+
)2+ -a,
-a,
当a> 时,a-1>-
时,a-1>- ,函数在[a-1,+∞)上单调递增,
,函数在[a-1,+∞)上单调递增,
g(x)min=g(a-1)=(a-1)2,
②当x≤a-1时,g(x)=x2-x-1+a=(x- )2+a-
)2+a- ,
,
如果a-1> 即a>
即a> 时,g(x)min=g(
时,g(x)min=g( )=a-
)=a- ,
,
如果a-1≤ 即a≤
即a≤ 时,g(x)在(-∞,a-1)上为减函数,g(x)min=g(a-1)=(a-1)2,
时,g(x)在(-∞,a-1)上为减函数,g(x)min=g(a-1)=(a-1)2,
当a> 时,(a-1)2-(a-
时,(a-1)2-(a- )=(a-
)=(a- )2>0,
)2>0,
综合可得,当 <a≤
<a≤ 时,g(x)的最小值是(a-1)2;
时,g(x)的最小值是(a-1)2;
当a> 时,g(x)的最小值是a-
时,g(x)的最小值是a- .
.
分析:(1)由于f(x)= -1,于是可得f(x)+f(2a-x)+2=0,与x取值无关得证;
-1,于是可得f(x)+f(2a-x)+2=0,与x取值无关得证;
(2)由定义域为[a+12,a+1],得 ,再由f(x)=
,再由f(x)= -1即可求解.
-1即可求解.
(3)根据题意,可得g(x)=x2+|x+1-a|,(x≠a),进而分①x≥a-1且x≠a与②x≤a-1两种情况讨论,由二次函数的性质,分别求出每种情况下f(x)的最小值,综合可得答案.
点评:本题考查函数的最值的求法及其意义,(2)关键在于对f(x)的化简,(3)的关键是根据二次函数的性质,进行分类讨论求g(x)的最值.
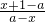 =
= -1,
-1,∴f(2a-x)=
 -1=-
-1=- -1,
-1,∴f(x)+f(2a-x)+2=
 +(-
+(- )-2+2=0,与x取值无关.
)-2+2=0,与x取值无关.∴f(x)+f(2a-x)+2=0对定义域内的所有x都成立;
(2)证明:∵f(x)的定义域为
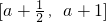 ,
,∴-1-a≤-x≤-a-
 ,-1≤a-x≤-
,-1≤a-x≤- ,-2≤
,-2≤ ≤-1,
≤-1,又f(x)=
 -1,
-1,∴-3≤
 -1≤-2,即f(x)的值域为[-3,-2].
-1≤-2,即f(x)的值域为[-3,-2].(3)解:函数g(x)=x2+|x+1-a|,(x≠a),
①当x≥a-1且x≠a时,g(x)=x2+x+1-a=(x+
 )2+
)2+ -a,
-a,当a>
 时,a-1>-
时,a-1>- ,函数在[a-1,+∞)上单调递增,
,函数在[a-1,+∞)上单调递增,g(x)min=g(a-1)=(a-1)2,
②当x≤a-1时,g(x)=x2-x-1+a=(x-
 )2+a-
)2+a- ,
,如果a-1>
 即a>
即a> 时,g(x)min=g(
时,g(x)min=g( )=a-
)=a- ,
,如果a-1≤
 即a≤
即a≤ 时,g(x)在(-∞,a-1)上为减函数,g(x)min=g(a-1)=(a-1)2,
时,g(x)在(-∞,a-1)上为减函数,g(x)min=g(a-1)=(a-1)2,当a>
 时,(a-1)2-(a-
时,(a-1)2-(a- )=(a-
)=(a- )2>0,
)2>0,综合可得,当
 <a≤
<a≤ 时,g(x)的最小值是(a-1)2;
时,g(x)的最小值是(a-1)2;当a>
 时,g(x)的最小值是a-
时,g(x)的最小值是a- .
.分析:(1)由于f(x)=
 -1,于是可得f(x)+f(2a-x)+2=0,与x取值无关得证;
-1,于是可得f(x)+f(2a-x)+2=0,与x取值无关得证;(2)由定义域为[a+12,a+1],得
 ,再由f(x)=
,再由f(x)= -1即可求解.
-1即可求解.(3)根据题意,可得g(x)=x2+|x+1-a|,(x≠a),进而分①x≥a-1且x≠a与②x≤a-1两种情况讨论,由二次函数的性质,分别求出每种情况下f(x)的最小值,综合可得答案.
点评:本题考查函数的最值的求法及其意义,(2)关键在于对f(x)的化简,(3)的关键是根据二次函数的性质,进行分类讨论求g(x)的最值.

练习册系列答案
相关题目
