题目内容
已知各项为正数的等差数列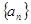 满足
满足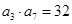 ,
,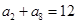 ,且
,且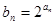 (
(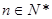 ).
).
(Ⅰ)求数列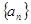 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列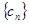 的前n项和
的前n项和 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)根据等差数列的性质, ,解关于
,解关于 、
、 的方程组,再求公差
的方程组,再求公差 ,从而便得结论;(Ⅱ)有已知条件得出,
,从而便得结论;(Ⅱ)有已知条件得出, ,再分组求和,即把
,再分组求和,即把 看作一个等差数列
看作一个等差数列 与一个等比数列
与一个等比数列 的前
的前 项的和之和.
项的和之和.
试题解析:(Ⅰ)  是等差数列,
是等差数列, ,
,  ,或
,或 , 4分
, 4分
又 ,
, . 6分
. 6分
(Ⅱ) ,
, ,
,
 9分
9分

 . 12分
. 12分
考点:等差数列的性质,等差、等比数列的求和公式,分组求和法.

练习册系列答案
相关题目
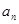 }中,
}中, ,公比
,公比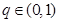 ,且
,且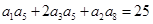 ,
,  与
与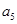 的等比中项为2.
的等比中项为2.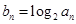 ,求:数列{
,求:数列{ }的前
}的前 项和为
项和为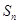 ,
,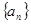 ,
,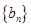 的通项
的通项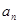 ,
,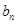 满足关系
满足关系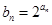 ,且数列
,且数列 项和
项和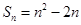
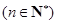 .
.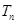 .
.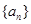 为递增等差数列,且
为递增等差数列,且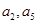 是方程
是方程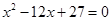 的两根.数列
的两根.数列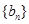 为等比数列,且
为等比数列,且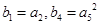 .
.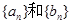 的通项公式;
的通项公式;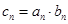 ,求数列
,求数列 的前
的前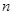 项和
项和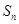 .
. 满足:
满足: ,
, .
. 及
及 的第n项为
的第n项为 ,若
,若 成等差数列,且
成等差数列,且 ,设数列
,设数列 的前
的前 项和
项和 .求数列
.求数列 }中,
}中, =3,前7项和
=3,前7项和 =28.
=28. }为等比数列,且
}为等比数列,且 ,
, 求数列
求数列 的前n项和
的前n项和
 .
.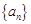 的前n项和为Sn,且
的前n项和为Sn,且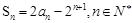 .
. ,记数列
,记数列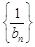 的前
的前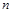 项和为
项和为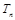 .求证:
.求证: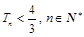 .
. 的前
的前 项和
项和 (
( ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,求使得
,求使得 成立的最小正整数
成立的最小正整数