题目内容
已知△ABC, ,
,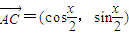 ,其中
,其中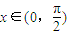 .
.(Ⅰ)求
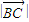 和△ABC的边BC上的高h;
和△ABC的边BC上的高h;(Ⅱ)若函数
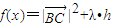 的最大值是5,求常数λ的值.
的最大值是5,求常数λ的值.
【答案】分析:(1)根据向量模的定义求出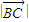 ,
,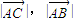 ,结合图象求出BC边上的高;
,结合图象求出BC边上的高;
(2)借助换元法把函数f(x)转换为二次函数g(t),结合二次函数的图象确定当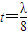 即λ=4时,函数f(x)的最大值为5.
即λ=4时,函数f(x)的最大值为5.
解答:解:(Ⅰ)∵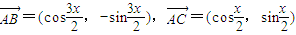 ,∴|
,∴|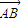 |=|
|=|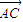 |=1
|=1
∴|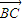 |=
|=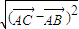 =
=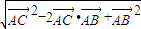 =
=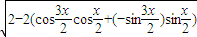
=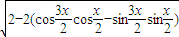 =
=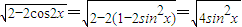 =2|sinx|
=2|sinx|
∵x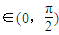 ,∴sinx∈(0,1),∴|
,∴sinx∈(0,1),∴|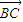 |=2sinx.
|=2sinx.
∵ ,△ABC是等腰三角形,
,△ABC是等腰三角形,
∴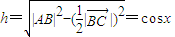
(Ⅱ)由(Ⅰ)知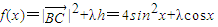 =4(1-cos2x)+λcosx=-4cos2x+λcosx+4
=4(1-cos2x)+λcosx=-4cos2x+λcosx+4
令t=cosx,∵x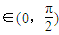 ,∴t∈(0,1)
,∴t∈(0,1)
则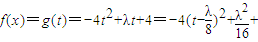 4
4
结合函数g(t)的图象可知
当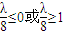 ,即λ≤0或λ≥8时,函数g(t)无最值.
,即λ≤0或λ≥8时,函数g(t)无最值.
当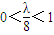 ,即0<λ<8时,f(x)max=
,即0<λ<8时,f(x)max=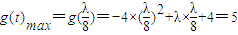
解得λ=4或λ=-4(舍)
故λ=4时,函数f(x)的最大值为5.
点评:本题考查了向量模的概念及求法、两角和的余弦、同角的三角函数关系,培养了学生等价转换及分类讨论、数形结合的数学解题能力.
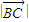 ,
,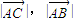 ,结合图象求出BC边上的高;
,结合图象求出BC边上的高;(2)借助换元法把函数f(x)转换为二次函数g(t),结合二次函数的图象确定当
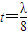 即λ=4时,函数f(x)的最大值为5.
即λ=4时,函数f(x)的最大值为5.解答:解:(Ⅰ)∵
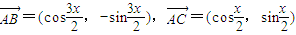 ,∴|
,∴|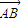 |=|
|=|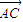 |=1
|=1∴|
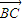 |=
|=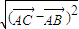 =
=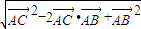 =
=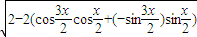
=
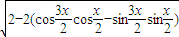 =
=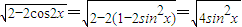 =2|sinx|
=2|sinx|∵x
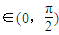 ,∴sinx∈(0,1),∴|
,∴sinx∈(0,1),∴|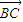 |=2sinx.
|=2sinx.∵
 ,△ABC是等腰三角形,
,△ABC是等腰三角形,∴
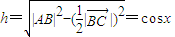
(Ⅱ)由(Ⅰ)知
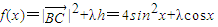 =4(1-cos2x)+λcosx=-4cos2x+λcosx+4
=4(1-cos2x)+λcosx=-4cos2x+λcosx+4令t=cosx,∵x
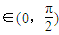 ,∴t∈(0,1)
,∴t∈(0,1)则
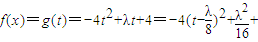 4
4结合函数g(t)的图象可知
当
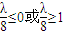 ,即λ≤0或λ≥8时,函数g(t)无最值.
,即λ≤0或λ≥8时,函数g(t)无最值.当
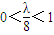 ,即0<λ<8时,f(x)max=
,即0<λ<8时,f(x)max=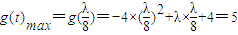
解得λ=4或λ=-4(舍)
故λ=4时,函数f(x)的最大值为5.
点评:本题考查了向量模的概念及求法、两角和的余弦、同角的三角函数关系,培养了学生等价转换及分类讨论、数形结合的数学解题能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

