题目内容
已知向量
，函数
.
⑴设
，x为某三角形的内角，求
时x的值;
⑵设
，当函数
取最大值时，求cos2x的值.
⑴
；⑵
解析试题分析：首先由数量积公式得
.⑴将，代入可得
，将化一得
，即
，
又因为
为三角形的内角，所以
；⑵将代入可得
，当且仅当
时，函数
.此时，所以
.
试题解析：由题可知，，
⑴当时，
，
∵
∴
∵为三角形的内角，∴ .6分
⑵当时，
，
当且仅当时，函数。
此时
∴ .12分
考点：1、数列的递推公式；2、等比数列.
练习册系列答案
阅读快车系列答案
相关题目
的终边与单位圆交于点P（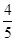
，
）.
、
、
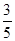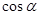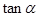值；
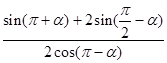的值.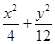 
＝1上在第一象限的点，A(2，0)，B(0，2
)
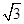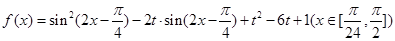其最小值为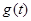
.
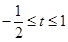时，要使关于
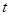的方程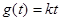
有一个实根，求实数
的取值范围．
的最大值，并写出
时的取值集合；
中，角
的对边分别为
，若
求
的最小值.
．
的最小正周期和值域；
中，角
的对边分别为
，若
且
，
，求
和
．
，且
，求
的值。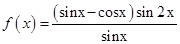
. 
的定义域及最小正周期；
-
sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为
.
]上的最大值和最小值.