题目内容
函数f(x)=
是定义在(-∞,+∞)上的奇函数,且f(1)=
(1)求实数c和d,并确定函数f(x)的解析式;
(2)判断f(x)在(-1,1)上的单调性,并用定义证明你的结论.
| cx+d |
| 1+x2 |
| 1 |
| 2 |
(1)求实数c和d,并确定函数f(x)的解析式;
(2)判断f(x)在(-1,1)上的单调性,并用定义证明你的结论.
(1)函数f(x)=
是定义在(-∞,+∞)上的奇函数,
可得f(0)=0,解得d=0.
再由f(1)=
=
,可得 c=1.
故函数的解析式为 f(x)=
.
(2)由函数的解析式可得函数在(-1,1)上是增函数.
证明:设-1<x1<x2<1,则 f(x1)-f(x2)=
-
=
=
=
.
由题设可得 x1-x2<0,1-x1x2>0,∴
<0,
故有f(x1)-f(x2)<0,即 f(x1)<f(x2),故函数在(-1,1)上是增函数.
| cx+d |
| 1+x2 |
可得f(0)=0,解得d=0.
再由f(1)=
| c |
| 2 |
| 1 |
| 2 |
故函数的解析式为 f(x)=
| x |
| 1+x2 |
(2)由函数的解析式可得函数在(-1,1)上是增函数.
证明:设-1<x1<x2<1,则 f(x1)-f(x2)=
| x1 |
| 1+x12 |
| x2 |
| 1+x22 |
=
| x1(1+x22)-x2(1+x12) |
| (1+x12)(1+x22) |
| x1-x2+x1•x2(x2-x1) |
| (1+x12)(1+x22) |
| ( x1-x2)(1-x1x2) |
| (1+x12)(1+x22) |
由题设可得 x1-x2<0,1-x1x2>0,∴
| ( x1-x2)(1-x1x2) |
| (1+x12)(1+x22) |
故有f(x1)-f(x2)<0,即 f(x1)<f(x2),故函数在(-1,1)上是增函数.

练习册系列答案
相关题目
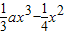 +cx+d(a,c,d∈R)满足f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立.
+cx+d(a,c,d∈R)满足f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立.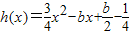 ,解不等式f'(x)+h(x)<0;
,解不等式f'(x)+h(x)<0; +cx+d(a,c,d∈R)满足f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立.
+cx+d(a,c,d∈R)满足f(0)=0,f'(1)=0,且f'(x)≥0在R上恒成立.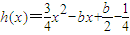 ,解不等式f'(x)+h(x)<0;
,解不等式f'(x)+h(x)<0;