题目内容
9.已知sinα+cosα=$\sqrt{2}$,求下列各式的值:(1)sinαcosα;
(2)sin3α+cos3α;
(3)sin4α+cos4α;
(4)sin4α-cos4α.
分析 (1)由sinα+cosα=$\sqrt{2}$两边同时平方可得1+2sinαcosα=2,从而可得sinαcosα=$\frac{1}{2}$;
(2)sin3α+cos3α=(sinα+cosα)(sin2α-sinαcosα+cos2α)结合sinαcosα=$\frac{1}{2}$,及sin2α+cos2α=1代入可求;
(3)sin4α+cos4α=(sin2α+cos2α)2-2(sinαcosα)2结合sinαcosα=$\frac{1}{2}$,及sin2α+cos2α=1代入可求;
(4)利用平方差公式结合sinαcosα=$\frac{1}{2}$,及sin2α+cos2α=1代入可求.
解答 解:(1)∵sinα+cosα=$\sqrt{2}$,
两边同时平方可得,1+2sinαcosα=2,
∴sinαcosα=$\frac{1}{2}$.
(2)sin3α+cos3α=(sinα+cosα)(sin2α-sinαcosα+cos2α)
=$\sqrt{2}$(1-$\frac{1}{2}$)=$\frac{\sqrt{2}}{2}$.
(3)sin4α+cos4α=(sin2α+cos2α)2-2(sinαcosα)2
=1-2×($\frac{1}{2}$)2=$\frac{1}{2}$.
(4)sin4α-cos4α=(sin2α+cos2α)(sin2α-cos2α)=sin2α-cos2α=(sinα+cosα)(sinα-cosα)=$\sqrt{2}$×$\sqrt{1-2sinαcosα}$=0.
点评 本题主要考查了同角平方关系的应用,解题中要注意一些常见式子的变形形式,属于公式的基本应用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
20.下列各角中,是第一象限角的是( )
| A. | 1200° | B. | -1140° | C. | -1350° | D. | 1850° |
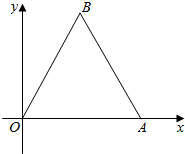 正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.
正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.