题目内容
若函数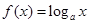
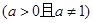 在
在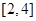 上的最大值与最小值之差为2,则
上的最大值与最小值之差为2,则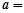 .
.
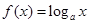
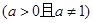 在
在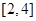 上的最大值与最小值之差为2,则
上的最大值与最小值之差为2,则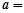 .
.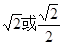 .
.试题分析:因为函数
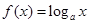
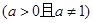 在
在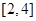 是单调函数,所以其最大值与最小值必在区间端点取到。由最大值与最小值之差为2,得
是单调函数,所以其最大值与最小值必在区间端点取到。由最大值与最小值之差为2,得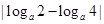 =2,即
=2,即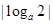 =2,解得a为
=2,解得a为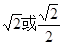 。
。点评:简单题,利用对数函数是单调函数,建立a的方程。

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
题目内容
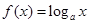
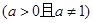 在
在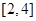 上的最大值与最小值之差为2,则
上的最大值与最小值之差为2,则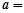 .
.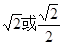 .
.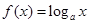
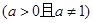 在
在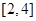 是单调函数,所以其最大值与最小值必在区间端点取到。由最大值与最小值之差为2,得
是单调函数,所以其最大值与最小值必在区间端点取到。由最大值与最小值之差为2,得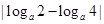 =2,即
=2,即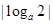 =2,解得a为
=2,解得a为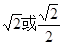 。
。
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案