题目内容
6.已知a,b是空间两条异面直线,它们所成的角为80°,过空间一点P作直线l,使l与a,b所成角均为50°,这样的l有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 在空间取一点P,经过点P分别作a∥a',b∥b',设直线a'、b'确定平面α.由异面直线所成角的定义,得a'、b'所成锐角等于80°,经过P的直线PM的射影P在a'、b'所成锐角的平分线上时,存在两条直线与a',b'所成的角都是50°,当PM的射影PQ在a'、b'所成钝角的平分线上时,存在1条直线与a',b'所成的角都是50°,由此可得本题答案.
解答 解:在空间取一点P,经过点P分别作a∥a',b∥b',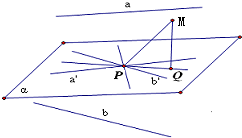
设直线a'、b'确定平面α,
当直线PM满足它的射影PQ在a'、b'所成角的平分线上时,
PM与a'所成的角等于PM与b'所成的角
因为直线a,b所成的角为80°,得a'、b'所成锐角等于80°
所以当PM的射影PQ在a'、b'所成锐角的平分线上时,
PM与a'、b'所成角的范围是[40°,90°).
这种情况下,过点P有两条直线与a',b'所成的角都是50°
当PM的射影PQ在a'、b'所成钝角的平分线上时,PM与a'、b'所成角的范围是[50°,90°).
这种情况下,过点P有且只有一条直线(即PM?α时)与a',b'所成的角都是50°
综上所述,过空间任意一点P可作与a,b所成的角都是50°的直线有3条
故选:C.
点评 本题给出两条直线所成角为80°,求过空间一点P可作与a,b所成的角都是50°的直线的条数.着重考查了空间两条异面直线所成角及其求法等知识,属于中档题.

练习册系列答案
相关题目
17.函数y=sin(x-$\frac{π}{3}$)的一个递增区间是( )
| A. | [-$\frac{5π}{6}$,$\frac{π}{6}$] | B. | [-$\frac{π}{6}$,$\frac{5π}{6}$] | C. | [-$\frac{π}{2}$,$\frac{π}{2}$] | D. | [-$\frac{π}{3}$,$\frac{2π}{3}$] |
18.${sin^2}\frac{π}{12}-{cos^2}\frac{π}{12}$的结果是( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |