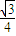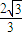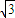题目内容
直线L经过双曲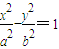 (a>0,b>0)右焦点F与其一条渐近线垂直且垂足为A,与另一条渐近线交于B点,
(a>0,b>0)右焦点F与其一条渐近线垂直且垂足为A,与另一条渐近线交于B点,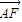 =
=
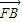 ,则双曲线的离心率为( )
,则双曲线的离心率为( )A.
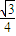
B.
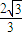
C.
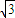
D.2
【答案】分析:设一渐近线OA的方程为 y= x,设A(m,
x,设A(m, ),B(n,-
),B(n,- ),由
),由  =
=
 ,求得点A的坐标,再由FA⊥OA,斜率之积等于-1,求出a2=3b2,代入e=
,求得点A的坐标,再由FA⊥OA,斜率之积等于-1,求出a2=3b2,代入e= =
= 进行运算.
进行运算.
解答:解:由题意得右焦点F(c,0),设一渐近线OA的方程为 y= x,则另一渐近线OB的方程为 y=-
x,则另一渐近线OB的方程为 y=- x,
x,
设A(m, ),B(n,-
),B(n,- ),∵
),∵ =
=
 ,∴(c-m,-
,∴(c-m,- )=
)= (n-c,-
(n-c,- ),
),
∴c-m= ,-
,- =-
=- ,∴m=
,∴m= ,n=
,n= ,
,
∴A( ,
, ).由FA⊥OA可得,斜率之积等于-1,即
).由FA⊥OA可得,斜率之积等于-1,即  =-1,
=-1,
∴a2=3b2,∴e= =
= =
= ,
,
故选B.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,求得点A的坐标是解题的关键.
 x,设A(m,
x,设A(m, ),B(n,-
),B(n,- ),由
),由  =
=
 ,求得点A的坐标,再由FA⊥OA,斜率之积等于-1,求出a2=3b2,代入e=
,求得点A的坐标,再由FA⊥OA,斜率之积等于-1,求出a2=3b2,代入e= =
= 进行运算.
进行运算.解答:解:由题意得右焦点F(c,0),设一渐近线OA的方程为 y=
 x,则另一渐近线OB的方程为 y=-
x,则另一渐近线OB的方程为 y=- x,
x,设A(m,
 ),B(n,-
),B(n,- ),∵
),∵ =
=
 ,∴(c-m,-
,∴(c-m,- )=
)= (n-c,-
(n-c,- ),
),∴c-m=
 ,-
,- =-
=- ,∴m=
,∴m= ,n=
,n= ,
,∴A(
 ,
, ).由FA⊥OA可得,斜率之积等于-1,即
).由FA⊥OA可得,斜率之积等于-1,即  =-1,
=-1,∴a2=3b2,∴e=
 =
= =
= ,
,故选B.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,求得点A的坐标是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 (a>0,b>0)右焦点F与其一条渐近线垂直且垂足为A,与另一条渐近线交于B点,
(a>0,b>0)右焦点F与其一条渐近线垂直且垂足为A,与另一条渐近线交于B点, =
=
 ,则双曲线的离心率为
,则双曲线的离心率为


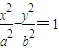 (a>0,b>0)右焦点F与其一条渐近线垂直且垂足为A,与另一条渐近线交于B点,
(a>0,b>0)右焦点F与其一条渐近线垂直且垂足为A,与另一条渐近线交于B点,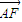 =
=
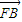 ,则双曲线的离心率为( )
,则双曲线的离心率为( )