题目内容
设函数 ,(a∈R).
,(a∈R).
(1)若a=1,证明:当x>﹣1时,f(x)≥0;
(2)若f(x)≤0在[0,+∞)上恒成立,求实数a的取值范围;
(3)设n∈N且n>1求证: .
.
 ,(a∈R).
,(a∈R).(1)若a=1,证明:当x>﹣1时,f(x)≥0;
(2)若f(x)≤0在[0,+∞)上恒成立,求实数a的取值范围;
(3)设n∈N且n>1求证:
 .
.(1)证明:a=1时, x>﹣1时,f(x)≥0,即
x>﹣1时,f(x)≥0,即 ,
,
亦即1﹣(x+1)e﹣x≥0,即ex≥x+1
因此只要证当x>﹣1时,ex≥x+1
构造函数g(x)=ex﹣x﹣1,
∴g′(x)=ex﹣1
当x≥0时,g′(x)≥0;
当﹣1<x<0时,g′(x)<0
∴g(x)在[0,+∞)上单调增,(﹣1,0]上单调减
∴g(x)min=g(0)=0
∴g(x)≥0,即当x>﹣1时,ex≥x+1
∴当x>﹣1时,f(x)≥0;
(2)解:f(x)≤0在[0,+∞)上恒成立,等价于x≥0时, 恒成立
恒成立
∵1﹣e﹣x∈[0,1),
∴
∴若x=0时,0=0,此时a∈R;
若x>0,ax+1>0,
∴ ,
,
∴a≥0 ∴a≥0,
x≥0时, 恒成立,等价于(1﹣e﹣x)(ax+1)﹣x≤0恒成立
恒成立,等价于(1﹣e﹣x)(ax+1)﹣x≤0恒成立
令h(x)=(1﹣e﹣x)(ax+1)﹣x,
∴h′(x)=a(1﹣e﹣x)+(ax+1)e﹣x﹣1
∴h″(x)=e﹣x(2a﹣ax﹣1)
∵a≥0,x≥0,
∴h″(x)≤(2a﹣1)e﹣x
①若2a﹣1≤0,即 时,h″(x)≤0,
时,h″(x)≤0,
∴h′(x)在[0,+∞)上单调减,
∴h′(x)≤h(0)=0,
∴h(x)在[0,+∞)上单调减,
∴h(x)≤h(0)=0,
∴f(x)≤0,满足题意;
②若2a﹣1>0,即 时,当
时,当 时,h''(x)>0,
时,h''(x)>0,
∴h′(x)在[0,+∞)上单调增,
∴h′(x)>h(0)=0,
∴h(x)在[0,+∞)上单调增,
∴h(x)>h(0)=0,
∴f(x)>0,不满足题意;
综上知,实数a的取值范围为 ;
;
(3)证明:由(2)知,当a= 时,
时, ,
,
∴ ,
,
当x∈(0,2)时, ,
,
∴ 令
令 ,
,
∴ ,
,
∴
∴ ,
,
∴
∴
∴
 x>﹣1时,f(x)≥0,即
x>﹣1时,f(x)≥0,即 ,
,亦即1﹣(x+1)e﹣x≥0,即ex≥x+1
因此只要证当x>﹣1时,ex≥x+1
构造函数g(x)=ex﹣x﹣1,
∴g′(x)=ex﹣1
当x≥0时,g′(x)≥0;
当﹣1<x<0时,g′(x)<0
∴g(x)在[0,+∞)上单调增,(﹣1,0]上单调减
∴g(x)min=g(0)=0
∴g(x)≥0,即当x>﹣1时,ex≥x+1
∴当x>﹣1时,f(x)≥0;
(2)解:f(x)≤0在[0,+∞)上恒成立,等价于x≥0时,
 恒成立
恒成立∵1﹣e﹣x∈[0,1),
∴

∴若x=0时,0=0,此时a∈R;
若x>0,ax+1>0,
∴
 ,
,∴a≥0 ∴a≥0,
x≥0时,
 恒成立,等价于(1﹣e﹣x)(ax+1)﹣x≤0恒成立
恒成立,等价于(1﹣e﹣x)(ax+1)﹣x≤0恒成立令h(x)=(1﹣e﹣x)(ax+1)﹣x,
∴h′(x)=a(1﹣e﹣x)+(ax+1)e﹣x﹣1
∴h″(x)=e﹣x(2a﹣ax﹣1)
∵a≥0,x≥0,
∴h″(x)≤(2a﹣1)e﹣x
①若2a﹣1≤0,即
 时,h″(x)≤0,
时,h″(x)≤0,∴h′(x)在[0,+∞)上单调减,
∴h′(x)≤h(0)=0,
∴h(x)在[0,+∞)上单调减,
∴h(x)≤h(0)=0,
∴f(x)≤0,满足题意;
②若2a﹣1>0,即
 时,当
时,当 时,h''(x)>0,
时,h''(x)>0,∴h′(x)在[0,+∞)上单调增,
∴h′(x)>h(0)=0,
∴h(x)在[0,+∞)上单调增,
∴h(x)>h(0)=0,
∴f(x)>0,不满足题意;
综上知,实数a的取值范围为
 ;
;(3)证明:由(2)知,当a=
 时,
时, ,
,∴
 ,
,当x∈(0,2)时,
 ,
,∴
 令
令 ,
,∴
 ,
,∴

∴
 ,
,∴

∴

∴


练习册系列答案
相关题目
 ,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是 . ,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 . ,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)<(x-2)lgm在区间[1,+∞)上恒成立,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)<(x-2)lgm在区间[1,+∞)上恒成立,则实数a的取值范围是 .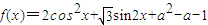 ,(a∈R)
,(a∈R)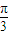 ]时,求f(x)的最大值.
]时,求f(x)的最大值.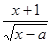 (a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。
(a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。