题目内容
已知数列{an},{bn}满足a1=1,且an,an+1是函数 的两个零点,则b10等于
的两个零点,则b10等于
- A.24
- B.32
- C.48
- D.64
D
分析:由韦达定理,得出 ,所以
,所以 ,两式相除得
,两式相除得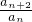 =2,数列{an}中奇数项成等比数列,偶数项也成等比数列.求出a10,a11后,先将即为b10.
=2,数列{an}中奇数项成等比数列,偶数项也成等比数列.求出a10,a11后,先将即为b10.
解答:由已知, ,所以
,所以 ,
,
两式相除得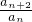 =2
=2
所以a1,a3,a5,…成等比数列,a2,a4,a6,…成等比数列.而a1=1,a2=2,
所以a10=2×24=32.a11=1×25=32,
又an+an+1=bn+1,
所以b10=a10+a11=64
故选D
点评:本题考查了韦达定理的应用,等比数列的判定及通项公式求解,考查转化、构造、计算能力.
分析:由韦达定理,得出
 ,所以
,所以 ,两式相除得
,两式相除得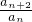 =2,数列{an}中奇数项成等比数列,偶数项也成等比数列.求出a10,a11后,先将即为b10.
=2,数列{an}中奇数项成等比数列,偶数项也成等比数列.求出a10,a11后,先将即为b10.解答:由已知,
 ,所以
,所以 ,
,两式相除得
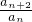 =2
=2所以a1,a3,a5,…成等比数列,a2,a4,a6,…成等比数列.而a1=1,a2=2,
所以a10=2×24=32.a11=1×25=32,
又an+an+1=bn+1,
所以b10=a10+a11=64
故选D
点评:本题考查了韦达定理的应用,等比数列的判定及通项公式求解,考查转化、构造、计算能力.

练习册系列答案
相关题目