题目内容
11.已知x,y的取值如表所示:| x | 2 | 3 | 4 | 5 |
| y | 2.2 | 3.8 | 5.5 | 6.5 |
分析 根据表中数据,求出样本中心点($\overline{x}$,$\overline{y}$),代入回归直线方程即可求出a的值.
解答 解:根据表中数据,得;
$\overline{x}$=$\frac{1}{4}$(2+3+4+5)=$\frac{7}{2}$,
$\overline{y}$=$\frac{1}{4}$(2.2+3.8+5.5+6.5)=$\frac{9}{2}$,
∴回归直线方程$\widehat{y}$=1.46x+a过样本中心($\frac{7}{2}$,$\frac{9}{2}$);
∴实数a=$\frac{9}{2}$-1.46×$\frac{7}{2}$=-0.61.
故答案为:0.61.
点评 本题考查了计算平均数以及利用样本中心点求回归直线方程的应用问题,是基础题目.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
2.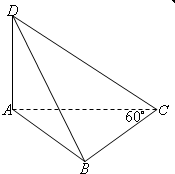 如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
 如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
20.已知随机变量X服从正态分布N(2,σ2),P(X≤3)=0.72,则P(1<X<3)等于( )
| A. | 0.28 | B. | 0.44 | C. | 0.56 | D. | 0.84 |
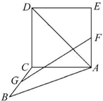 如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$. 为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.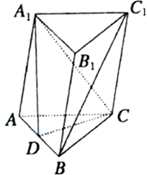 如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.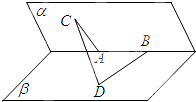 如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.