题目内容
已知函数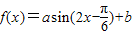
(1)若x∈
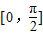 时f(x)的值域为[4,10],求a×b的值;
时f(x)的值域为[4,10],求a×b的值;(2)若a=1,求函数y=f(-x)的单调增区间.
【答案】分析:(1)x∈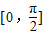 ,知-
,知-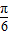
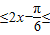
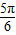 ,由x∈
,由x∈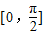 时,函数
时,函数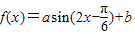 的值域为[4,10],知:当a>0时,
的值域为[4,10],知:当a>0时,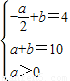 ;当a<0时,
;当a<0时, ,由此能求出a×b.
,由此能求出a×b.
(2)当a=1时,f(x)=sin(2x-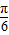 )+b,f(-x)=sin(-2x-
)+b,f(-x)=sin(-2x-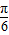 )+b,故函数y=f(-x)的单调增区间满足条件:-
)+b,故函数y=f(-x)的单调增区间满足条件:-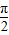 +2kπ≤-2x-
+2kπ≤-2x-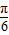 ≤
≤ +2kπ,k∈Z.由此能求出当a=1时,函数y=f(-x)的单调增区间.
+2kπ,k∈Z.由此能求出当a=1时,函数y=f(-x)的单调增区间.
解答:解:(1)∵x∈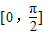 ,∴-
,∴-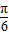
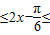
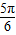 ,
,
∵x∈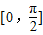 时,函数
时,函数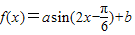 的值域为[4,10],
的值域为[4,10],
∴当a>0时,在2x-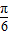 =-
=-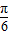 时,f(x)min=asin(-
时,f(x)min=asin(-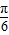 )+b=-
)+b=-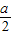 +b=4,
+b=4,
在2x-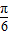 =
=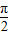 时,f(x)max=asin
时,f(x)max=asin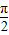 +b=a+b=10,
+b=a+b=10,
解方程组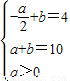 ,得a=4,b=6,
,得a=4,b=6,
∴a×b=24.
当a<0时,在2x-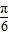 =-
=-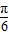 时,f(x)max=asin(-
时,f(x)max=asin(-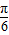 )+b=-
)+b=-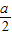 +b=10,
+b=10,
在2x-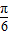 =
=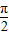 时,f(x)min=asin
时,f(x)min=asin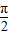 +b=a+b=4,
+b=a+b=4,
解方程组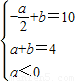 ,得a=-4,b=8,
,得a=-4,b=8,
∴a×b=-32.
(2)当a=1时,f(x)=sin(2x-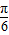 )+b,
)+b,
f(-x)=sin(-2x- )+b,
)+b,
∴函数y=f(-x)的单调增区间满足条件:-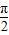 +2kπ≤-2x-
+2kπ≤-2x-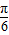 ≤
≤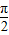 +2kπ,k∈Z.
+2kπ,k∈Z.
解得-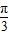 -kπ≤x≤
-kπ≤x≤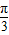 -kπ,k∈Z.
-kπ,k∈Z.
∴当a=1时,函数y=f(-x)的单调增区间为[- -kπ,
-kπ,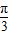 -kπ],k∈Z.
-kπ],k∈Z.
点评:本题考查三角函数的值域、单调区间的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.易错点是容易忽视a<0的情况.
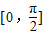 ,知-
,知-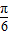
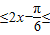
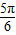 ,由x∈
,由x∈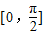 时,函数
时,函数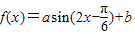 的值域为[4,10],知:当a>0时,
的值域为[4,10],知:当a>0时,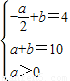 ;当a<0时,
;当a<0时, ,由此能求出a×b.
,由此能求出a×b.(2)当a=1时,f(x)=sin(2x-
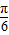 )+b,f(-x)=sin(-2x-
)+b,f(-x)=sin(-2x-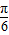 )+b,故函数y=f(-x)的单调增区间满足条件:-
)+b,故函数y=f(-x)的单调增区间满足条件:-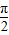 +2kπ≤-2x-
+2kπ≤-2x-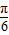 ≤
≤ +2kπ,k∈Z.由此能求出当a=1时,函数y=f(-x)的单调增区间.
+2kπ,k∈Z.由此能求出当a=1时,函数y=f(-x)的单调增区间.解答:解:(1)∵x∈
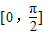 ,∴-
,∴-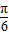
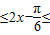
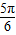 ,
,∵x∈
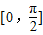 时,函数
时,函数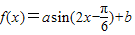 的值域为[4,10],
的值域为[4,10],∴当a>0时,在2x-
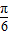 =-
=-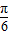 时,f(x)min=asin(-
时,f(x)min=asin(-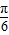 )+b=-
)+b=-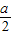 +b=4,
+b=4,在2x-
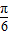 =
=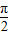 时,f(x)max=asin
时,f(x)max=asin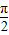 +b=a+b=10,
+b=a+b=10,解方程组
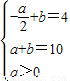 ,得a=4,b=6,
,得a=4,b=6,∴a×b=24.
当a<0时,在2x-
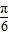 =-
=-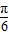 时,f(x)max=asin(-
时,f(x)max=asin(-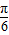 )+b=-
)+b=-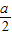 +b=10,
+b=10,在2x-
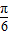 =
=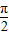 时,f(x)min=asin
时,f(x)min=asin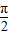 +b=a+b=4,
+b=a+b=4,解方程组
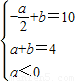 ,得a=-4,b=8,
,得a=-4,b=8,∴a×b=-32.
(2)当a=1时,f(x)=sin(2x-
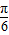 )+b,
)+b,f(-x)=sin(-2x-
 )+b,
)+b,∴函数y=f(-x)的单调增区间满足条件:-
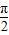 +2kπ≤-2x-
+2kπ≤-2x-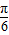 ≤
≤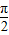 +2kπ,k∈Z.
+2kπ,k∈Z.解得-
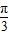 -kπ≤x≤
-kπ≤x≤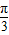 -kπ,k∈Z.
-kπ,k∈Z.∴当a=1时,函数y=f(-x)的单调增区间为[-
 -kπ,
-kπ,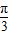 -kπ],k∈Z.
-kπ],k∈Z.点评:本题考查三角函数的值域、单调区间的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.易错点是容易忽视a<0的情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
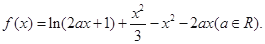
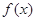 的极值点,求实数a的值;
的极值点,求实数a的值;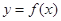 在
在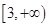 上为增函数,求实数a的取值范围.
上为增函数,求实数a的取值范围.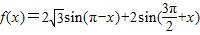
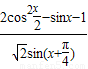 的值.
的值.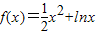
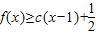 ,求c的取值范围.
,求c的取值范围.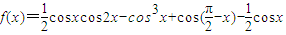
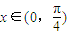 ,且
,且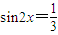 ,求f(x)的值.
,求f(x)的值.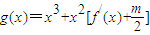 在区间(t,3)上有最值,求实数m取值范围;
在区间(t,3)上有最值,求实数m取值范围;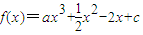
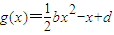 ,在(1)的条件下,是否存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由.
,在(1)的条件下,是否存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由.