题目内容

已知圆的方程x2+y2+kx+2y+k2=0,某一定点为(1,2),要使过点(1,2)所作圆的切线有两条,求k的取值范围.

-<k<,


解析:

圆的标准方程为(x+)2+(y+1)2=.

圆心为(-,-1),半径为(4-3k2>0).

过点(1,2)作圆的切线有两条,则必须满足

解得-<k<,

此为所求k的取值范围.

练习册系列答案
相关题目
已知圆的方程x2+y2=25，过M（-4，3）作直线MA，MB与圆交于点A，B，且MA，MB关于直线y=3对称，则直线AB的斜率等于（　　）
A、-
4
3
B、-
3
4
C、-
5
4
D、-
4
5
已知圆的方程x2+y2=25，过M（-4，3）作直线MA，MB与圆交于点A，B，且MA，MB关于直线y=3对称，则直线AB的斜率等于
 
．
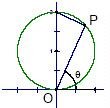精英家教网已知圆的方程x2+（y-1）2=1，P为圆上任意一点（不包括原点）．直线OP的倾斜角为θ弧度，|OP|=d，则d=f（θ）的图象大致为
 
已知圆的方程x2+y2=4，若抛物线过点A（0，-1），B（0，1）且以圆的切线为准线，则抛物线的焦点轨迹方程是（　　）
A、
x2
3
+
y2
4
=1（y≠0）
B、
x2
4
+
y2
3
=1（y≠0）
C、
x2
3
+
y2
4
=1（x≠0）
D、
x2
4
+
y2
3
=1（x≠0）
已知圆的方程x2+y2=4，若抛物线过定点A（0，1），B（0，-1）且以圆的切线为准线，则抛物线焦点的轨迹方程是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网