题目内容
.数列{a }满足S
}满足S =
2n-a
=
2n-a , n∈N
, n∈N
⑴计算a 、a
、a 、a
、a 、a
、a ,并由此猜想通项公式a
,并由此猜想通项公式a
(2)用数字归纳法证明(1)中的猜想.
【答案】
(1)a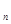 =
=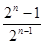 ( n∈N
( n∈N )
)
(2)略
【解析】解: (1) a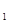 =1、a
=1、a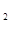 =
=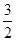 、a
、a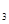 =
=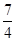 、a
、a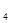 =
=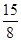
猜想a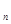 =
=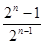 ( n∈N
( n∈N )
)
证明:①当n = 1时,a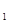 =
1结论成立
=
1结论成立
②假设n = K (K≥1)时,结论成立
即a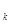 =
=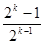 ,
那么n=k+1时
,
那么n=k+1时
a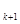 =S
=S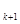 -S
-S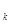 =2(k+1)
-a
=2(k+1)
-a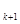 -2k+
-2k+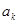
=2+a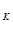 -a
-a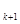
∴2 a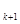 =2+ a
=2+ a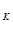
∴a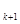 =
=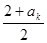 =
=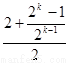 =
=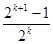
这表明n=k+1时,结论成立
∴a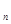 =
=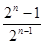

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
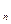 }满足S
}满足S
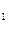 、a
、a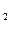 、a
、a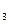 、a
、a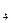 ,并由此猜想通项公式a
,并由此猜想通项公式a