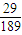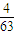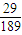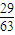Question

（理）从正方体的八个顶点确定的所有直线中任取两条，这两条直线是异面直线且成60°的概率是（　　）

• A、

  29

  189

• B、

  29

  63

• C、

  4

  63

• D、

  4

  7

Answer 1

分析：先通过观察正方体中的所有直线列出所有情况，让两条直线是异面直线且成60°的情况数除以总情况数即为所求的概率．

解答：解：因为从正方体的八个顶点中任取两个点共有C₈²=28条直线，
从中任意取出两条有C₂₈²种取法，
其中与一条面对角线成异面直线且成60°的直线有4条，
所以成异面直线且成角为60°的直线有（12×4）÷2=24对，
所以P=

24

C 2 28

=

4

63

．
故选C．

点评：本小题主要考查异面直线及其所成的角、异面直线及其应用、等可能事件的概率等基础知识，考查运算求解能力，考查数空间想象力．属于基础题．