题目内容
选做题:不等式选讲.
已知a,b,c是不全相等的正数,求证: ,并指出等号成立的条件.
,并指出等号成立的条件.
证明:∵a,b,c是不全相等的正数,∴ ,(2分)
,(2分)
故不等式等价于 ,即
,即 .(5分)
.(5分)
∵a,b,c>0,∴ ,不等式得证(8分)
,不等式得证(8分)
取号等条件是 ,即c2=ab且a、b、c互不相等的正数 (10分)
,即c2=ab且a、b、c互不相等的正数 (10分)
分析:由 ,故不等式等价于
,故不等式等价于  ,利用平均值不等式可证得此不等式成立.
,利用平均值不等式可证得此不等式成立.
点评:本题考查平均值不等式的应用,注意检验等号成立的条件.
 ,(2分)
,(2分)故不等式等价于
 ,即
,即 .(5分)
.(5分)∵a,b,c>0,∴
 ,不等式得证(8分)
,不等式得证(8分)取号等条件是
 ,即c2=ab且a、b、c互不相等的正数 (10分)
,即c2=ab且a、b、c互不相等的正数 (10分)分析:由
 ,故不等式等价于
,故不等式等价于  ,利用平均值不等式可证得此不等式成立.
,利用平均值不等式可证得此不等式成立.点评:本题考查平均值不等式的应用,注意检验等号成立的条件.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
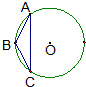 短长度为
短长度为 (2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)