题目内容
已知f(x)=
ax3+
bx2+cx,a＞0,m＞0,f′(
)＜0,
+
+ 
=0都成立.(1)若c＞0,证明f(x)在(0,1)内有极值;
(2)若c≤0,请问f(x)在(0,1)内是否有极值,请说明理由.
解: (Ⅰ)由得
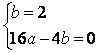由，∴ 解之得
即；
(Ⅱ) 
由题意，得f(0)=
,f(1)=
若
＞0,则f(0)＞0,又f(
)＜0,所以f(x)=0在(0，
)内有解;
若
≤0,则f(1)= 
=
(
(－
)+
=
＞0,
又f(
)＜0,所以f(x)=0在(
,1)内有解
综上所述: 方程f(x)=0在(0，1)内恒有解
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知f(x)=ax3+ln(
+x)+2，且f（-5）=m，则f（5）+f（-5）的值为（ ）
| x2+1 |
| A、4 | B、0 | C、2m | D、-m+4 |
已知f(x)=ax3+
(ab≠0)，对任意a，b∈R（a≠b），都有
＞0．若x1+x2＜0，且x1?x2＜0，则f（x1）+f（x2）的值（ ）
| b |
| x |
| f(a)-f(b) |
| a-b |
| A、恒小于0 | B、恒大于0 |
| C、可能为0 | D、可正可负 |