题目内容
如图,在正方体ABCD—A1B1C1D1中,求异面直线A1B与AC所成的角.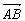
解：不妨设正方体的棱长为1,设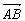=a,
=b,
=c,则|a|=|b|=|c|=1,a·b=b·c=c·a=0，?
=a-c，
=a+b.?
∴·
=（a-c）·（a+b）=|a|2+a·b-a·c-b·c=1，而|
|=|
|=
.?
∴cos〈,
〉=
=
,?
∴〈
,
〉=60°.?
因此,异面直线A1B与AC所成的角为60°.
练习册系列答案
相关题目
题目内容
如图,在正方体ABCD—A1B1C1D1中,求异面直线A1B与AC所成的角.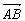
解：不妨设正方体的棱长为1,设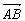=a, =b, =c,则|a|=|b|=|c|=1,a·b=b·c=c·a=0，?
=a-c，=a+b.?
∴·=（a-c）·（a+b）=|a|2+a·b-a·c-b·c=1，而||=||=.?
∴cos〈,〉==,?
∴〈,〉=60°.?
因此,异面直线A1B与AC所成的角为60°.
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体ABCD-A1B1C1D1中，E为DD1的中点，
如图，在正方体ABCD-A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的主视图与左视图的面积的比值为（ ）